vibration data from MIT study
Summary so far: a rigid body balanced on two bike tires has two primary oscillation mode: an even mode and an odd mode. The even mode is associated with the bike bouncing up and down on the two tires symmetrically. The odd mode is associated with the bike rotating on the tires: one tire compressed, the other expanded, then vice-versa. An estimation of my moment of inertia is that the root-mean-squared separation of mass from my center-of-gravity is around 39 cm. The half-wheelbase of my bike is 49.5 cm. Since the former is lower than the latter, the odd mode will have a higher oscillation frequency than the even mode, assuming the bike and body are rigid and the body is firmly attached to the bike.
The issue is that the body is not rigid and it is not firmly attached to the bike. A spring-mass model for the human body has been developed which shows how vibrations are attenuated between body parts (no snickering from the crowd: that wasn't modeled). The result of this is, the higher the frequency, the less the fraction of the body mass which is contribute to the "inertia" term in the spring-mass system. The mass ends up being frequency-dependent. In other words, it's complicated.
Spring-Mass Man: high frequencies fail to propagate up the spine.
So we come back to Champoux's result:
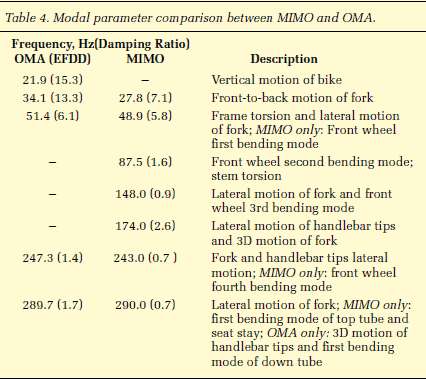Vibrational modes measured by Champoux. OMA: measured while riding on a treadmill; MIMO: measured with shakers on the front dropout and handlebars.
From this table, you'd expect frequencies above around 20 Hz would not be effectively transmitted from the road to the bike, although the bike contains a resonances at 34 and 51 Hz which might be a factor, depending on the nature of the impact and where the vibrations are measured.
As I already noted, Champoux rode his bike on a treadmill on which he'd attached a bump which he hit every 0.9 seconds or so. He moved accelerometers around the bike to search out the modes. Unfortunately he showed time-domain data only for the stem. I'm not so interested in vibrations at the stem, which can clearly flex, since the point of this whole exercise was to model what's happening at the pedal spindles.
Hastings, Blair, and Culligan @ MIT and Pober at UMass did a similar experiment in 2004, with Kevin Monahan (then US criterium champion) riding each of three Cervelo bikes set up with equivalent wheels and with essentially equivalent geometry, also on a treadmill with a bump. The bike hit the bump once per second. An accelerometer was attached to the base of the seatpost to measure vibrations. Here's a plot of a typical response:
accelerations over time measured by Hastings, et al., in response to first the front wheel, then the rear wheel, hitting a bump. Note the plot is mislabeled.
It stands to reason the acceleration spectrum at the pedal spindles would be similar. They saved me the work of doing a Fourier transform of their data. Here's a plot they made of the power spectrum (proportional to acceleration squared) for the three bikes, "CF" = carbon fiber, "AL" = aluminum, and "S" = steel:
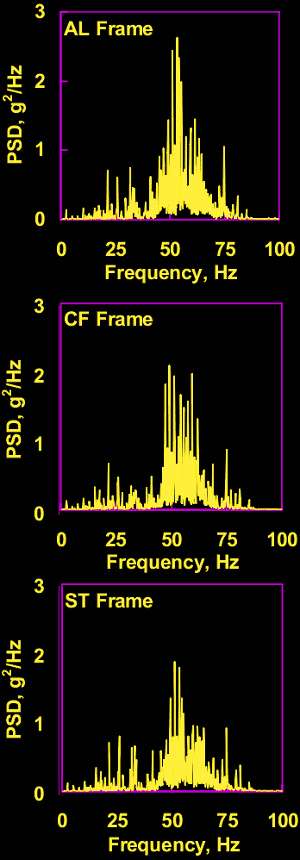vibration spectra measured at base of seat tube by Hastings, et al., in MIT study
Note the broad peak in the vicinity of 55 to 60 Hz. This corresponds nicely with Champoux's mode identified at 51.4 Hz: frame torsion and lateral motion of the fork. Since the fork is generally more flexible than the frame (as demonstrated in Tour Magazine tests), the fork will have a large influence on the frequency of this mode. Since the same fork model was used on each of the Cervelo test bikes, it is understandable that the spectra of the three bikes near this frequency are similar.
As an aside, the authors were particularly interested in how the frame materials affected the spectra. The carbon fiber dampen vibrations in the 30 Hz range, and Al has higher vibration magnitudes near the 55-60 Hz peak.
Anyway, it's clear the effect of vibration modes within the bike-body system are important. The vibration "noise" I constructed intuitively doesn't quite cut the mustard.
An interesting issue here is these vibration components show amplitudes exceeding 1 g. That means the seatpost, at least, experiences negative g's. So does the bike go flying? Well, peak displacement at a given frequency equals peak acceleration at that frequency divided by (2πf)². So at one g (9.8 m/sec²) at 50 Hz, the peak displacement is 0.1 mm. So the bike doesn't go flying: we're talking minor vibrations substantially less than the inflated tire thickness.
Anyway, I'm changing my noise model to better represent the importance of this oscillation mode near 55 Hz.
The issue is that the body is not rigid and it is not firmly attached to the bike. A spring-mass model for the human body has been developed which shows how vibrations are attenuated between body parts (no snickering from the crowd: that wasn't modeled). The result of this is, the higher the frequency, the less the fraction of the body mass which is contribute to the "inertia" term in the spring-mass system. The mass ends up being frequency-dependent. In other words, it's complicated.
Spring-Mass Man: high frequencies fail to propagate up the spine.So we come back to Champoux's result:
Vibrational modes measured by Champoux. OMA: measured while riding on a treadmill; MIMO: measured with shakers on the front dropout and handlebars.From this table, you'd expect frequencies above around 20 Hz would not be effectively transmitted from the road to the bike, although the bike contains a resonances at 34 and 51 Hz which might be a factor, depending on the nature of the impact and where the vibrations are measured.
As I already noted, Champoux rode his bike on a treadmill on which he'd attached a bump which he hit every 0.9 seconds or so. He moved accelerometers around the bike to search out the modes. Unfortunately he showed time-domain data only for the stem. I'm not so interested in vibrations at the stem, which can clearly flex, since the point of this whole exercise was to model what's happening at the pedal spindles.
Hastings, Blair, and Culligan @ MIT and Pober at UMass did a similar experiment in 2004, with Kevin Monahan (then US criterium champion) riding each of three Cervelo bikes set up with equivalent wheels and with essentially equivalent geometry, also on a treadmill with a bump. The bike hit the bump once per second. An accelerometer was attached to the base of the seatpost to measure vibrations. Here's a plot of a typical response:
accelerations over time measured by Hastings, et al., in response to first the front wheel, then the rear wheel, hitting a bump. Note the plot is mislabeled.It stands to reason the acceleration spectrum at the pedal spindles would be similar. They saved me the work of doing a Fourier transform of their data. Here's a plot they made of the power spectrum (proportional to acceleration squared) for the three bikes, "CF" = carbon fiber, "AL" = aluminum, and "S" = steel:
vibration spectra measured at base of seat tube by Hastings, et al., in MIT studyNote the broad peak in the vicinity of 55 to 60 Hz. This corresponds nicely with Champoux's mode identified at 51.4 Hz: frame torsion and lateral motion of the fork. Since the fork is generally more flexible than the frame (as demonstrated in Tour Magazine tests), the fork will have a large influence on the frequency of this mode. Since the same fork model was used on each of the Cervelo test bikes, it is understandable that the spectra of the three bikes near this frequency are similar.
As an aside, the authors were particularly interested in how the frame materials affected the spectra. The carbon fiber dampen vibrations in the 30 Hz range, and Al has higher vibration magnitudes near the 55-60 Hz peak.
Anyway, it's clear the effect of vibration modes within the bike-body system are important. The vibration "noise" I constructed intuitively doesn't quite cut the mustard.
An interesting issue here is these vibration components show amplitudes exceeding 1 g. That means the seatpost, at least, experiences negative g's. So does the bike go flying? Well, peak displacement at a given frequency equals peak acceleration at that frequency divided by (2πf)². So at one g (9.8 m/sec²) at 50 Hz, the peak displacement is 0.1 mm. So the bike doesn't go flying: we're talking minor vibrations substantially less than the inflated tire thickness.
Anyway, I'm changing my noise model to better represent the importance of this oscillation mode near 55 Hz.
Comments
P.S : I've been digging your posts but the black background is frankly a bit of an eyesore. I generally avoid reading blogs that play with your vision.
On comfort, there's two issues:
1. In the linear regime, what can be felt?
2. In the beyond-linear regime, ie significant hits, what can be felt?
Honestly, I don't know. Looking at the MIT data and "spring-mass man", I have a hard time believing you're going to feel anything too far into the acoustic range. 35 Hz already seems a real stretch to me, and that was where carbon fiber seemed to have the strongest effect. Yet people claim carbon fiber is smoother than Al. I really can't say. My carbon fiber bike may take hits better than my older Al frame (now cracked, RIP.... Champoux had some good work on that subject, as well), but the Al frame had a steeper head tube.
I test rode a Cannondale CAAD-9 a few months back and was shocked at how smooth it was on the appalling San Francisco streets in the SOMA district. If you'd have told me it was carbon, I'd have believed you, no problem.
Note the lowest order modes are from tires. So tire pressure is the #1 thing. Then fork bending is next. So fork compliance is next. Then of course geometry is important, as that affects the moments.
So the short version: "I don't know".