simulating Metrigear Vector cadence extraction (pt 4: orientation)
To extract cadence from accelerometer data is the accelerometers need to be properly oriented. So I constructed a simplistic scheme to extract the angle from the accelerations. It's super-simple: just accumulate average accelerations, then calculate a transformation rotation angle which beings one of them to zero.
Consider the following diagram:
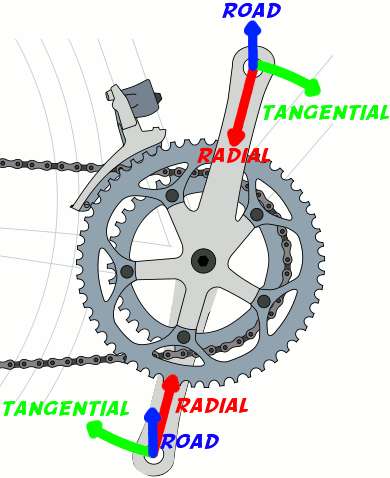
From the perspective of the spindle, radial acceleration is always in the same direction. Tangential (I seem to alternate between calling this "tangential" and "transverse") acceleration is also always in the same direction, as long as the crank rotation is consistently increasing (or consistently decreasing). I also show a vector for road vibration. It's easy to see this will tend to cancel out over time for each spindle. When the spindle rotates 180 degrees, it's in the opposite direction relative to the spindle. The same deal with acceleration in the direction of motion. When the spindle rotates 180 degrees, it flips.
Tangential acceleration may always be in the same direction as long as the cadence keeps increasing. But of course, it doesn't. Eventually cadence slows, and so over time, tangential acceleration also averages to zero. Only radial acceleration is never negative, except for "noise", which also averages to zero.
So the deal is, if I calculate an average for acceleration along each of two orthogonal coordinates, I can construct a vector from these components. Eventually I know the direction of this vector will converge on the radial direction, and I'm oriented.
One can do a bit better, though. By realizing the transverse acceleration will have a non-zero component proportional to the average rate of cadence change, I can tweak the result a bit. I tried this, and it didn't really help; the adjustment was small in comparison to the error from noise.
So I implemented the simpler approach in my Perl script. Here's the result for the the same eleven simulated "runs" I showed before, with the same noise. For each time point, I calculated the square root of the mean square of the error.
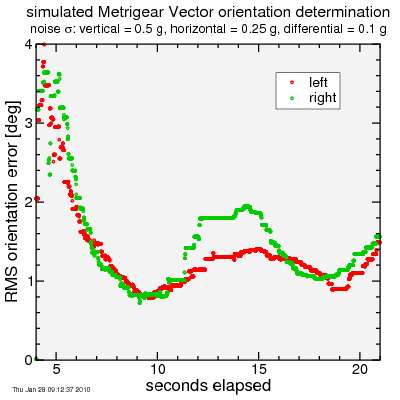
This error quickly drops below 2 degrees, then sort of hovers there, not fully converging to zero within the time scale of the simulation.
Less than 2 degrees seems fairly good. But is this good enough?
Consider I'm applying force to the pedal at 45 degrees relative to the propulsive (tangential) direction. In this case, 71% of the force is propulsive, 71% of the force is perpendicular to the propulsive direction (I know -- this doesn't add to 100%. That's vectors for you.) What if I'm off by 2 degrees? Well, in that case I make a 2.5% error in the calculation of propulsive power. Were the error 1 degree, this would be a 1.2% error. The goal is for error from all sources to be less than 1.5%, so even a 1.2% error is too much.
Furthermore, suppose my cadence is smooth and I'm riding on a smooth road during this time. I estimate cadence proportional to the square root of the radial acceleration. This results in a 0.03% error in cadence estimation. So that's a small error. The bigger deal in this example is the force component. For that, I need the orientation to be well within 1 degree accurate. I fail that in this test.
But the good news is these tests are relatively short. The longer I ride after reorienting the pedals, the better I can estimate the orientation. So within a minute or so, I should be good. And this example was for highly inconsistent pedal cadence. For smoother variation, it does better.
I have no idea how MetriGear does its orientation. This is just one approach which might be used. But even so, it's not too bad. Brim Brothers, as I've noted, don't have the luxury of sloppy techniques, as they need to reassess the orientation, almost from scratch, several times a second. That's a far tougher problem. If they can crack that, I'm confident Metrigear have the orientation issue under control.
Consider the following diagram:

From the perspective of the spindle, radial acceleration is always in the same direction. Tangential (I seem to alternate between calling this "tangential" and "transverse") acceleration is also always in the same direction, as long as the crank rotation is consistently increasing (or consistently decreasing). I also show a vector for road vibration. It's easy to see this will tend to cancel out over time for each spindle. When the spindle rotates 180 degrees, it's in the opposite direction relative to the spindle. The same deal with acceleration in the direction of motion. When the spindle rotates 180 degrees, it flips.
Tangential acceleration may always be in the same direction as long as the cadence keeps increasing. But of course, it doesn't. Eventually cadence slows, and so over time, tangential acceleration also averages to zero. Only radial acceleration is never negative, except for "noise", which also averages to zero.
So the deal is, if I calculate an average for acceleration along each of two orthogonal coordinates, I can construct a vector from these components. Eventually I know the direction of this vector will converge on the radial direction, and I'm oriented.
One can do a bit better, though. By realizing the transverse acceleration will have a non-zero component proportional to the average rate of cadence change, I can tweak the result a bit. I tried this, and it didn't really help; the adjustment was small in comparison to the error from noise.
So I implemented the simpler approach in my Perl script. Here's the result for the the same eleven simulated "runs" I showed before, with the same noise. For each time point, I calculated the square root of the mean square of the error.

This error quickly drops below 2 degrees, then sort of hovers there, not fully converging to zero within the time scale of the simulation.
Less than 2 degrees seems fairly good. But is this good enough?
Consider I'm applying force to the pedal at 45 degrees relative to the propulsive (tangential) direction. In this case, 71% of the force is propulsive, 71% of the force is perpendicular to the propulsive direction (I know -- this doesn't add to 100%. That's vectors for you.) What if I'm off by 2 degrees? Well, in that case I make a 2.5% error in the calculation of propulsive power. Were the error 1 degree, this would be a 1.2% error. The goal is for error from all sources to be less than 1.5%, so even a 1.2% error is too much.
Furthermore, suppose my cadence is smooth and I'm riding on a smooth road during this time. I estimate cadence proportional to the square root of the radial acceleration. This results in a 0.03% error in cadence estimation. So that's a small error. The bigger deal in this example is the force component. For that, I need the orientation to be well within 1 degree accurate. I fail that in this test.
But the good news is these tests are relatively short. The longer I ride after reorienting the pedals, the better I can estimate the orientation. So within a minute or so, I should be good. And this example was for highly inconsistent pedal cadence. For smoother variation, it does better.
I have no idea how MetriGear does its orientation. This is just one approach which might be used. But even so, it's not too bad. Brim Brothers, as I've noted, don't have the luxury of sloppy techniques, as they need to reassess the orientation, almost from scratch, several times a second. That's a far tougher problem. If they can crack that, I'm confident Metrigear have the orientation issue under control.

Comments