Drivetrain losses: Spicer's data
Recall Spicer did some nice drivetrain efficiency measurements, which he published in Human Power 50, 2000. His argument is that chain tension is an important parameter, that higher tension tends to yield higher efficiency. Here's his result again:
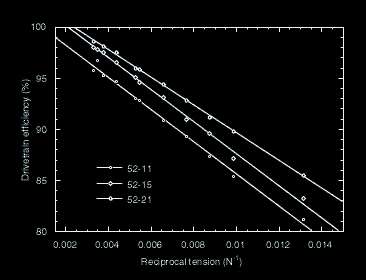Spicer's efficiency measurements as a function of reciprocal chain tension for each of three rear cogs
My model described dissipated power rather than drivetrain efficiency. To get efficiency (ν), I take the power dissipation as a function of T and divide it by power P, where T / P = chain speed = R L = C Nf L.
ν ≡ 1 ‒ Pdt / P = 1 ‒ (K / L) [1/Nf + 1/Nr + 2 (T0 / T) (1/Nf + 1/Nr + 2/Nd)] ‒ Kd / (Nd T L).
Spicer says efficiency depends on T but is independent of chain speed. However, since Spicer uses a conatant Nf, for him constant chain speed simply means constant C. the above equation is indeed independent of C. Furthermore, Spicer says ν is well fit by a formula ν = ν∞ ‒ α / T for some constant ν∞ and slope α. This equation also has this form. So it is fully consistent with Spicer.
Here's where things don't work so well. The intercept predicted by Spicer for infinite tension is above 100% efficiency. Bummer. This implies you could use a bike chain to construct a perpepetual motion machine. Allen comments on Spicer's data in the next issue of the journal. He asserts Spicer's approach was flawed in that he is determining drivetrain losses by comparing torques at the crank and at the hub. Small errors in one or both could easily translate into large errors in the difference. Better would be to use a device which directly measured the difference in torque. So the result of this is you can't rely on Spicer's extrapolated infinite-tension efficiency. Instead of using Spicer's values directly, it's tempting to assume he has a fixed error in his reported efficiencies.
So from my equations I come up with the "true" infinite-tension efficiency:
ν∞ = 1 ‒ (K / L) [1/Nf + 1/Nr].
To compare to Spicer's values, I then apply a fixed error term:
ν∞,Spicer = 1 + Δν ‒ (K / L) [1/Nf + 1/Nr].
There's two unknowns parameters here ( Δν and K ) for which I have 3 data points (intercepts of 11, 15, and 21 tooth cogs).
That was the infinite-tension limit Additionally, there's the slope term, which describss how efficiency drops with 1/T. For that I have:
α = 2 (K/L) T0 (1/Nf + 1/Nr + 2/Nd) + Kd / Nd L.
This shows a relatively weaker dependence on the cog choice, since 2 Nf/Nd is going to be relatively larger than the other two terms, since Nd is typically 11 - 12 teeth (although some riders are using 13 teeth or even 15 teeth for increased efficiency).
Red derailleur modified by Dark Albert with 15-tooth pulley
Least-square fits to the Spicer data are as follows:
I fit these to the model. From the intercepts, which I plot versus 1/Nf + 1/Nr. The slope gives me K / L, the intercept Δν.
The results:
Δν = 0.066,
K / L = 0.447,
which yields K = 5.68 mm.
Now before moving further, this is already raising a big fat red flag. Δν = 6.6? How could that be? I already showed data published in Wilson that drivetrain efficiencies are typically in the 97-98% range. How could Spicer's data be off by as much as 6.6%? I'm starting to question my assumption of a fixed efficiency offset.
But what about K/L? Does that make any sense? This requires considering what the model means. The total bending angle of a link when it bends = 2π / N, where N is the number of teeth (or, if you prefer, 360° / N). The model says dissipation from this bending = K Ttot / N, where Ttot is the total chain tension (T0 or T + T0 in my model). So K is the equivalent distance associated with a full rotation of a chain link, assuming drag = Ttot. The radius of a chain pin is approximately 2 mm, so the circumference is approximately 12.6 mm. Thus the drag force is less than the effective tension: the proportionality factor is represents a coefficient of friction of 45%. A reference for the coefficient of drag for two steel surfaces coated by thin oxide films is 27%, but with clean surfaces it is 78%. This number falls between the two. But what about oil, you ask? Spicer found lubrication was a minor factor in chain drag. At the contact points, the lubrication is largely repelled from the pressure. So the purpose of the lubrication is more to keep the chain from rusting than it is to reduce friction. Anyway, this number certainly doesn't seem out of line.
Okay, onward: despite the issue with Δν, I forge ahead to the slope parameter. Here's a plot of α versus 1/Nf + 1/Nr + 2/Nd.
Unfortunately the data don't fall onto a nice straight line. So I needed help. The slope here depends on T0, while the intercept describes the rolling friction of the pulleys, Kd. So I'll cheat a bit and use data reported in the WeightWeenies forum:
Further tests by SKF, and confirmed by the Danish cycle magazine Cykel Magasinet (Sep 2005), describe dramatic reductions in friction compared to conventional cycle bearings. For example:
With a pair of race wheels (total of six bearings), friction with ceramic bearings is reduced 22 fold While Dura Ace pulleys consume 0.78W @ 500rpm, ceramic pulleys use less than 0.06W A Record BB @ 100rpm and 400W consumes 0.6W, the same BB with ceramic bearings consumes 0.02W
Conveniently, Spicer used a Dura-Ace derailleur. So given the test rotation rate of rpm, converting to 8.33 rotations per second, I get:
Kd = 94 mJ/rev
That was for the Dura-Ace pulleys. For the Ceramic, the number would be 2.4 mJ/rev.
Then I did a constrained linear fit on the data, yielding:
2 (K / L) T0 = 50.65 N,
or since we already solved for K / L, so it's easy enough to solve:
T0 = 56.65 N.
So how's this compare with typical values of T? Suppose I weigh 60 kg with clothing. That's around 600 N. If I stand on the pedal when the crank is at 3 o'clock, that's a chain tension of 1000 N, assuming 170 mm cranks with a 50 tooth front ring, with the half-inch tooth spacing. So it says the chain bending resistance at the top of the crank is around 18 times bigger than the bending resistance at the bottom of the crank.
But there remains that pesky issue of Δν. With that so large, the Spicer model is assured to over-predict drivetrain losses. I'm not sure what to do about that. Or does something magically happen at low values of 1/T that cause the slope (as plotted by Spicer) to suddenly flatten?
Spicer's efficiency measurements as a function of reciprocal chain tension for each of three rear cogsMy model described dissipated power rather than drivetrain efficiency. To get efficiency (ν), I take the power dissipation as a function of T and divide it by power P, where T / P = chain speed = R L = C Nf L.
ν ≡ 1 ‒ Pdt / P = 1 ‒ (K / L) [1/Nf + 1/Nr + 2 (T0 / T) (1/Nf + 1/Nr + 2/Nd)] ‒ Kd / (Nd T L).
Spicer says efficiency depends on T but is independent of chain speed. However, since Spicer uses a conatant Nf, for him constant chain speed simply means constant C. the above equation is indeed independent of C. Furthermore, Spicer says ν is well fit by a formula ν = ν∞ ‒ α / T for some constant ν∞ and slope α. This equation also has this form. So it is fully consistent with Spicer.
Here's where things don't work so well. The intercept predicted by Spicer for infinite tension is above 100% efficiency. Bummer. This implies you could use a bike chain to construct a perpepetual motion machine. Allen comments on Spicer's data in the next issue of the journal. He asserts Spicer's approach was flawed in that he is determining drivetrain losses by comparing torques at the crank and at the hub. Small errors in one or both could easily translate into large errors in the difference. Better would be to use a device which directly measured the difference in torque. So the result of this is you can't rely on Spicer's extrapolated infinite-tension efficiency. Instead of using Spicer's values directly, it's tempting to assume he has a fixed error in his reported efficiencies.
So from my equations I come up with the "true" infinite-tension efficiency:
ν∞ = 1 ‒ (K / L) [1/Nf + 1/Nr].
To compare to Spicer's values, I then apply a fixed error term:
ν∞,Spicer = 1 + Δν ‒ (K / L) [1/Nf + 1/Nr].
There's two unknowns parameters here ( Δν and K ) for which I have 3 data points (intercepts of 11, 15, and 21 tooth cogs).
That was the infinite-tension limit Additionally, there's the slope term, which describss how efficiency drops with 1/T. For that I have:
α = 2 (K/L) T0 (1/Nf + 1/Nr + 2/Nd) + Kd / Nd L.
This shows a relatively weaker dependence on the cog choice, since 2 Nf/Nd is going to be relatively larger than the other two terms, since Nd is typically 11 - 12 teeth (although some riders are using 13 teeth or even 15 teeth for increased efficiency).
Red derailleur modified by Dark Albert with 15-tooth pulleyLeast-square fits to the Spicer data are as follows:
I fit these to the model. From the intercepts, which I plot versus 1/Nf + 1/Nr. The slope gives me K / L, the intercept Δν.
The results:
Δν = 0.066,
K / L = 0.447,
which yields K = 5.68 mm.
Now before moving further, this is already raising a big fat red flag. Δν = 6.6? How could that be? I already showed data published in Wilson that drivetrain efficiencies are typically in the 97-98% range. How could Spicer's data be off by as much as 6.6%? I'm starting to question my assumption of a fixed efficiency offset.
But what about K/L? Does that make any sense? This requires considering what the model means. The total bending angle of a link when it bends = 2π / N, where N is the number of teeth (or, if you prefer, 360° / N). The model says dissipation from this bending = K Ttot / N, where Ttot is the total chain tension (T0 or T + T0 in my model). So K is the equivalent distance associated with a full rotation of a chain link, assuming drag = Ttot. The radius of a chain pin is approximately 2 mm, so the circumference is approximately 12.6 mm. Thus the drag force is less than the effective tension: the proportionality factor is represents a coefficient of friction of 45%. A reference for the coefficient of drag for two steel surfaces coated by thin oxide films is 27%, but with clean surfaces it is 78%. This number falls between the two. But what about oil, you ask? Spicer found lubrication was a minor factor in chain drag. At the contact points, the lubrication is largely repelled from the pressure. So the purpose of the lubrication is more to keep the chain from rusting than it is to reduce friction. Anyway, this number certainly doesn't seem out of line.
Okay, onward: despite the issue with Δν, I forge ahead to the slope parameter. Here's a plot of α versus 1/Nf + 1/Nr + 2/Nd.
Unfortunately the data don't fall onto a nice straight line. So I needed help. The slope here depends on T0, while the intercept describes the rolling friction of the pulleys, Kd. So I'll cheat a bit and use data reported in the WeightWeenies forum:
Further tests by SKF, and confirmed by the Danish cycle magazine Cykel Magasinet (Sep 2005), describe dramatic reductions in friction compared to conventional cycle bearings. For example:
With a pair of race wheels (total of six bearings), friction with ceramic bearings is reduced 22 fold While Dura Ace pulleys consume 0.78W @ 500rpm, ceramic pulleys use less than 0.06W A Record BB @ 100rpm and 400W consumes 0.6W, the same BB with ceramic bearings consumes 0.02W
Conveniently, Spicer used a Dura-Ace derailleur. So given the test rotation rate of rpm, converting to 8.33 rotations per second, I get:
Kd = 94 mJ/rev
That was for the Dura-Ace pulleys. For the Ceramic, the number would be 2.4 mJ/rev.
Then I did a constrained linear fit on the data, yielding:
2 (K / L) T0 = 50.65 N,
or since we already solved for K / L, so it's easy enough to solve:
T0 = 56.65 N.
So how's this compare with typical values of T? Suppose I weigh 60 kg with clothing. That's around 600 N. If I stand on the pedal when the crank is at 3 o'clock, that's a chain tension of 1000 N, assuming 170 mm cranks with a 50 tooth front ring, with the half-inch tooth spacing. So it says the chain bending resistance at the top of the crank is around 18 times bigger than the bending resistance at the bottom of the crank.
But there remains that pesky issue of Δν. With that so large, the Spicer model is assured to over-predict drivetrain losses. I'm not sure what to do about that. Or does something magically happen at low values of 1/T that cause the slope (as plotted by Spicer) to suddenly flatten?
Comments
So combining this with the lower mass for the compact makes that the winning choice for me.
My impression from Spicer and the re-analysis by Walker is that higher chain tension is more efficient. Walker seems to be saying that the greater efficiency of the higher chain tension of smaller cogs/rings would outweigh the efficiency increase of less chain bend.
But you seem to be saying the opposite? Higher chain tension is less efficient? Maybe I'm reading this all wrong.