Metrigear Vector versus Brim Brothers
Brim Brothers just published an update on their status, the first one since Eurobike last year. Brim Brothers system looks very promising: put the force sensors in the cleat of the cycling shoe. That sounds a lot like Metrigear Vector, right?
Well, not quite. I've made a large number of posts here about the Vector, as it's fun trying to figure out how it works. But there's a very important difference between the two.
This is hinted at in the Brim Brothers blog post:
The most important (and most fun) part of the algorithm is taking the accelerometer data and using it to work out cadence, crank angle and pedal angle at each sample point. This is the same kind of technology that allows a Wii control or an iPhone to detect movements, but we need to use it to measure complex rotational movements very accurately. Having the accelerometer attached to the cleat/shoe (which rocks back and forth by an unpredictable amount all the time) makes this a lot more complex than, say, having the accelerometer fixed inside the pedal spindle. But if we did that then you wouldn’t be able to just step off one bike and onto another and have the power meter come with you…
But if we did that then you wouldn’t be able to just step off one bike and onto another and have the power meter come with you…
To measure power, you need the component of force in the propulsive direction. This requires you know the orientation of the cleat relative to the direction of pedal motion. With a shoe, this direction is constantly changing. It's changing not just in inertial space due to "ankling", but relative to the propulsive direction as the crank rotates. Terribly complicated.
On the other hand, as I've pointed out many times, the pedal spindle is always oriented the same relative to the propulsive direction. Once you figure out which that direction is, and I described already how one might do that, you're good to go until the pedal is adjusted. And if the pedal is adjusted, for example tightened or moved to a different bike, it would take only a few crank rotations for the system to figure out something's up and reorient itself. Recall in the tangential direction, the average acceleration over time goes to zero, while in the radial direction, the orbital acceleration is always non-negative and therefore averages to greater than zero. So if you can determine in which direction accelerations average to zero, and which orthogonal direction they average to greater than zero, you're oriented. I described all of this before in a long series of posts: nothing new.
So with Vector it's easier to determine which direction is the propulsive direction, and which is the radial direction. Only the propulsive direction contributes to power.
But power is force times speed, or equivalently torque times rotation rate. I get torque from force by knowing the crank length. Brim Brothers claims to allow you to jump from one bike to another, so it needs to figure out crank length. With Vector, you tell it the crank length, which makes its computational life all that much easier. In any case, you still then need to know rotation rate. The obvious way to rotation rate is via the orbital acceleration, ω²L, where ω is the angular velocity and L is the crank length. That acceleration can be measured every sample, providing a high-resolution reading on rotation rate.
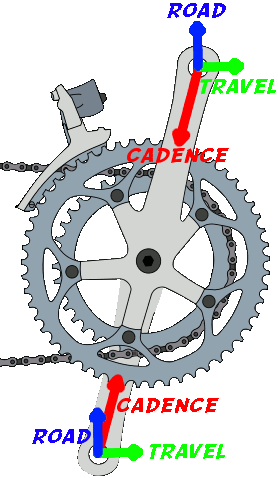
acceleration vectors at pedals: travel is from bike moving forward, road is from road vibration (for example), cadence is from pedals rotating.
The issue is that it's not the only acceleration in town. First there's the accelerations of the bike as it moves, turns, and/or responds to road grade changes. But additionally there's "vibration noise". I also did a number of posts on vibration. Vibration can come directly from the road, or the road can excite vibrational modes in the bike-body system. In either case, the pedals vibrate. They need to differentiate that acceleration from the orbital acceleration which provides the rotation rate, a critical element for power.
Sure, you can measure rotation rate separately, for example with a cadence sensor magnet. But these typically tell the average rotation rate over an entire pedal stroke. That's not good enough: you'd then need to assume something about the rotation rate within the pedal stroke. That won't be perfectly uniform. And for example when climbing and other "low-inertia" situations like riding through sand or into a headwind, the variation in rotation rate may well be correlated with applied power. So the assumption of uniform pedal rotation through a pedal stroke may yield a systematic power error.
But the nice thing about Vector is that we know the orientations of the two spindles. Road vibrations, accelerations, even most frame vibrational modes will all move the two pedal spindles in the same direction. On the other hand, the rotational accelerations are always in the opposite directions, assuming cranks 180 degrees apart. So subtract one from the other and magically road vibration, linear acceleration associated with the bike traveling forward, all that junk goes away. Brim Brothers is going to have a much tougher time with this. It gets even tougher the more types of float the pedal allows.
So the Vector has advantages in both determining the direction of forces and in determining the rate of pedal rotation. Errors in either quickly eat into the error budget for power determination. And when you're trying to hit a 2% error margin under all conditions, paved or unpaved, sprinting or cruising, climbing or descending, you need any advantage you can get.
So I wish the Brim Brothers the best. But they've got a tough challenge ahead of them, even tougher than Metrigear's.
Well, not quite. I've made a large number of posts here about the Vector, as it's fun trying to figure out how it works. But there's a very important difference between the two.
This is hinted at in the Brim Brothers blog post:
The most important (and most fun) part of the algorithm is taking the accelerometer data and using it to work out cadence, crank angle and pedal angle at each sample point. This is the same kind of technology that allows a Wii control or an iPhone to detect movements, but we need to use it to measure complex rotational movements very accurately. Having the accelerometer attached to the cleat/shoe (which rocks back and forth by an unpredictable amount all the time) makes this a lot more complex than, say, having the accelerometer fixed inside the pedal spindle.
To measure power, you need the component of force in the propulsive direction. This requires you know the orientation of the cleat relative to the direction of pedal motion. With a shoe, this direction is constantly changing. It's changing not just in inertial space due to "ankling", but relative to the propulsive direction as the crank rotates. Terribly complicated.
On the other hand, as I've pointed out many times, the pedal spindle is always oriented the same relative to the propulsive direction. Once you figure out which that direction is, and I described already how one might do that, you're good to go until the pedal is adjusted. And if the pedal is adjusted, for example tightened or moved to a different bike, it would take only a few crank rotations for the system to figure out something's up and reorient itself. Recall in the tangential direction, the average acceleration over time goes to zero, while in the radial direction, the orbital acceleration is always non-negative and therefore averages to greater than zero. So if you can determine in which direction accelerations average to zero, and which orthogonal direction they average to greater than zero, you're oriented. I described all of this before in a long series of posts: nothing new.
So with Vector it's easier to determine which direction is the propulsive direction, and which is the radial direction. Only the propulsive direction contributes to power.
But power is force times speed, or equivalently torque times rotation rate. I get torque from force by knowing the crank length. Brim Brothers claims to allow you to jump from one bike to another, so it needs to figure out crank length. With Vector, you tell it the crank length, which makes its computational life all that much easier. In any case, you still then need to know rotation rate. The obvious way to rotation rate is via the orbital acceleration, ω²L, where ω is the angular velocity and L is the crank length. That acceleration can be measured every sample, providing a high-resolution reading on rotation rate.

acceleration vectors at pedals: travel is from bike moving forward, road is from road vibration (for example), cadence is from pedals rotating.
The issue is that it's not the only acceleration in town. First there's the accelerations of the bike as it moves, turns, and/or responds to road grade changes. But additionally there's "vibration noise". I also did a number of posts on vibration. Vibration can come directly from the road, or the road can excite vibrational modes in the bike-body system. In either case, the pedals vibrate. They need to differentiate that acceleration from the orbital acceleration which provides the rotation rate, a critical element for power.
Sure, you can measure rotation rate separately, for example with a cadence sensor magnet. But these typically tell the average rotation rate over an entire pedal stroke. That's not good enough: you'd then need to assume something about the rotation rate within the pedal stroke. That won't be perfectly uniform. And for example when climbing and other "low-inertia" situations like riding through sand or into a headwind, the variation in rotation rate may well be correlated with applied power. So the assumption of uniform pedal rotation through a pedal stroke may yield a systematic power error.
But the nice thing about Vector is that we know the orientations of the two spindles. Road vibrations, accelerations, even most frame vibrational modes will all move the two pedal spindles in the same direction. On the other hand, the rotational accelerations are always in the opposite directions, assuming cranks 180 degrees apart. So subtract one from the other and magically road vibration, linear acceleration associated with the bike traveling forward, all that junk goes away. Brim Brothers is going to have a much tougher time with this. It gets even tougher the more types of float the pedal allows.
So the Vector has advantages in both determining the direction of forces and in determining the rate of pedal rotation. Errors in either quickly eat into the error budget for power determination. And when you're trying to hit a 2% error margin under all conditions, paved or unpaved, sprinting or cruising, climbing or descending, you need any advantage you can get.
So I wish the Brim Brothers the best. But they've got a tough challenge ahead of them, even tougher than Metrigear's.

Comments