changing setback
I took a break from thinking about the Metrigear Vector to think a bit about position, after the subject came up in BikeTech Review.
Position's a tricky deal. Move the saddle forward and you feel like sliding back. Then move the saddle back and you feel like riding on the nose. Saddle fore-aft must be dialed in, right?
Wrong.
The reason is when you change the fore-aft position of the saddle, you're changing other things as well. For example, the distance from the saddle to the bars.
Keith Bontrager has an interesting article on position, based on physics. His argument is the key thing is to get your center-of-mass positioned correctly for good handling in the different orientations you typically find yourself. The bike should be balanced in the saddle, out of the saddle sprinting, and out of the saddle climbing. I might add descending is another position which counts. But if you have the right center of mass relative to the bottom bracket, and the right bottom bracket relative to the front and rear wheels, everything should be good.
From a physiological perspective, body position can be dialed in, then the body in that fixed position rotated about the bottom bracket to give the correct center of mass orientation. Assume here that the body position is dialed, and the you're making an adjustment on fore-aft center-of-mass position.
Here's a diagram of my position from a photo I took pedaling the trainer a few years ago, when I was still riding my trusty Fuji Team Mercury-issue Teschner-built Al frame (ah, the good old days, when I worried less about bike mass and spent more time actually riding!)
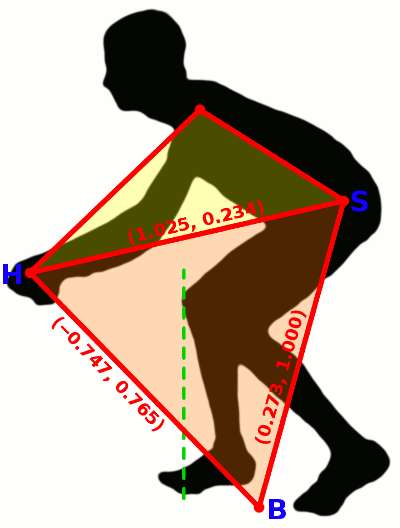
To get this outline, I first rotated the original photo so the line connecting the hubs was horizontal.
First note the green dashed line: that goes from the front of the crank in a vertical line. Andy Pruitt says this line should come close to the front of the knee. It does in my case, so I pass this test.
But suppose I follow Bontrager's prescription and I want to adjust my position, anyway, after analyzing my center of mass. Focus on the lower triangle (B-S-H). Assume for the sake of this post my body angles are dialed in. So I want to rotate this triangle without changing any of the side lengths (which will also preserve each of the angles: surely you remember the Law of Sines!). Then if I keep the lower triangle unchanged, it's easy to see the upper triangle will be unchanged as well, rotating with the lower triangle. So I don't need to worry about the upper triangle.
The plot shows the length of the run and rise of each line segment, normalized to the high of the hip socket above the bottom bracket. From these dimensions, I can define coordinates, placing the bottom bracket at the origin.
(0, 0): position of bottom bracket
(xS, yS): position of hip socket
(xH, yH): position of hands
Suppose I want to hips back by Δx in these coordinates. If I were to do this and leave it at that, everything would go amok. With the change in xS, I also need to change yS, xH, and yH.
I could worry about angles, or as I noted referring to the Law of Sines, just the side lengths. I'll take that approach.
First the seat: I started with coordinates (xS, yS) for the hip socket. I want the distance to the hip from the bottom bracket to be the same. That's equivalent to the square of the distance to the hip socket to be the same. Therefore:
(xS + Δx)² + (yS + ΔyS)² = xS² + yS²
Expanding the left to first order, then subtracting off xS² + yS² from each side, then dividing by two yields:
ΔyS = ‒Δx (xS / yS)
So I need to lower my seat by a 27% the amount I moved the saddle back (this in x-y coordinates: I'd need to adjust for the seat tube angle).
I want to avoid sines, cosines, and tangents in this analysis, so I'll stick with distances. I now need to move the hand position to maintain both the distance to the bottom bracket and the distance to the hip socket. This involves two unknowns (ΔxH and ΔyH) and two equations.
The first equation:
ΔyH yH = ‒ΔxH xH
and the second equation:
(ΔxH ‒ Δx) (xH ‒ xS) =
‒(ΔyH ‒ ΔyS) (yH ‒ yS).
I can multiply all terms by yS then plug in the previous solution for the seat position:
ΔyS yS = ‒Δx xS,
yielding
(ΔxH ‒ Δx) (xH ‒ xS) yS =
‒(yS ΔyH + xS Δx) (yH ‒ yS),
which eliminates ΔyS. I now have a choice of solving for either ΔxH or ΔyH. I'll choose the latter, first multiplying top and bottom by xH then plugging in the first equation, then eliminating minus signs from each side (I hate minus signs):
(ΔyH yH + Δx xH) (xH ‒ xS) yS =
(yS ΔyH + xS Δx) (yH ‒ yS) xH.
Good: this is one equation and one unknown, so it's simple algebra.
(ΔyH yH + Δx xH) (xH ‒ xS) yS ‒
(yS ΔyH + xS Δx) (yH ‒ yS) xH = 0.
Now collect terms in ΔyH and Δx:
ΔyH yS [yH (xH ‒ xS) ‒ xH (yH ‒ yS)] =
Δx xH [xS (yH ‒ yS) ‒ yS (xH ‒ xS)].
Some of those terms cancel! (If I'd had my eyes open I'd have noticed this sooner!)
ΔyH yS (xH yS ‒ yH xS) =
Δx xH [xS yH ‒ yS xH].
Then the bracketed terms differ only in sign:
ΔyH yS = ‒Δx xH
Or, simply enough:
ΔyH = ‒Δx xH / yS.
So using my parameters, I want to move my handlebars up 74.7% the amount I moved the seat back (again, in x-y coordinates: I need to adjust for head tube and seat tube angles).
It's then simple to solve for ΔxH:
ΔxH = Δx yH / yS,
which for my coordinates yields ΔxH / Δx = 76.5%.
So in summary, if I move my seat back 1 cm, I would also want to move it down 2.7 mm. I'd then want to move my bars up 7.5 mm and back 7.7 mm.
But I'm not quite done yet... Suppose my seat angle and head tube angle are both 74 degrees. This is what I measured from the photo (obviously a fairly crude measurement) and I don't recall the dimensions of the Fuji. Okay -- finally time for some trig. I then need to move the post down by 2.7 mm / sin 74° = 3 mm, then move the saddle back on the rails by 1 cm + 2.7 mm / tan 74° = 11 mm. Similarly, with the handlebars, I'd need to add 7.5 mm / sin 74° = 8 mm of spacers to the handlebar. And I'd ideally decrease my stem length by 7.7 mm ‒ 7,5 mm / tan 74° = 5.5 mm.
It might be tough getting the 5 mm shorter stem. But I can also get a stem of the same length and a different angle to bring the bars up and closer. I'll leave it here, though. The main point is a simple shift back on the saddle, to be properly evaluated, requires changes to both coordinates of both primary contact points.
Position's a tricky deal. Move the saddle forward and you feel like sliding back. Then move the saddle back and you feel like riding on the nose. Saddle fore-aft must be dialed in, right?
Wrong.
The reason is when you change the fore-aft position of the saddle, you're changing other things as well. For example, the distance from the saddle to the bars.
Keith Bontrager has an interesting article on position, based on physics. His argument is the key thing is to get your center-of-mass positioned correctly for good handling in the different orientations you typically find yourself. The bike should be balanced in the saddle, out of the saddle sprinting, and out of the saddle climbing. I might add descending is another position which counts. But if you have the right center of mass relative to the bottom bracket, and the right bottom bracket relative to the front and rear wheels, everything should be good.
From a physiological perspective, body position can be dialed in, then the body in that fixed position rotated about the bottom bracket to give the correct center of mass orientation. Assume here that the body position is dialed, and the you're making an adjustment on fore-aft center-of-mass position.
Here's a diagram of my position from a photo I took pedaling the trainer a few years ago, when I was still riding my trusty Fuji Team Mercury-issue Teschner-built Al frame (ah, the good old days, when I worried less about bike mass and spent more time actually riding!)

To get this outline, I first rotated the original photo so the line connecting the hubs was horizontal.
First note the green dashed line: that goes from the front of the crank in a vertical line. Andy Pruitt says this line should come close to the front of the knee. It does in my case, so I pass this test.
But suppose I follow Bontrager's prescription and I want to adjust my position, anyway, after analyzing my center of mass. Focus on the lower triangle (B-S-H). Assume for the sake of this post my body angles are dialed in. So I want to rotate this triangle without changing any of the side lengths (which will also preserve each of the angles: surely you remember the Law of Sines!). Then if I keep the lower triangle unchanged, it's easy to see the upper triangle will be unchanged as well, rotating with the lower triangle. So I don't need to worry about the upper triangle.
The plot shows the length of the run and rise of each line segment, normalized to the high of the hip socket above the bottom bracket. From these dimensions, I can define coordinates, placing the bottom bracket at the origin.
(0, 0): position of bottom bracket
(xS, yS): position of hip socket
(xH, yH): position of hands
Suppose I want to hips back by Δx in these coordinates. If I were to do this and leave it at that, everything would go amok. With the change in xS, I also need to change yS, xH, and yH.
I could worry about angles, or as I noted referring to the Law of Sines, just the side lengths. I'll take that approach.
First the seat: I started with coordinates (xS, yS) for the hip socket. I want the distance to the hip from the bottom bracket to be the same. That's equivalent to the square of the distance to the hip socket to be the same. Therefore:
(xS + Δx)² + (yS + ΔyS)² = xS² + yS²
Expanding the left to first order, then subtracting off xS² + yS² from each side, then dividing by two yields:
ΔyS = ‒Δx (xS / yS)
So I need to lower my seat by a 27% the amount I moved the saddle back (this in x-y coordinates: I'd need to adjust for the seat tube angle).
I want to avoid sines, cosines, and tangents in this analysis, so I'll stick with distances. I now need to move the hand position to maintain both the distance to the bottom bracket and the distance to the hip socket. This involves two unknowns (ΔxH and ΔyH) and two equations.
The first equation:
ΔyH yH = ‒ΔxH xH
and the second equation:
(ΔxH ‒ Δx) (xH ‒ xS) =
‒(ΔyH ‒ ΔyS) (yH ‒ yS).
I can multiply all terms by yS then plug in the previous solution for the seat position:
ΔyS yS = ‒Δx xS,
yielding
(ΔxH ‒ Δx) (xH ‒ xS) yS =
‒(yS ΔyH + xS Δx) (yH ‒ yS),
which eliminates ΔyS. I now have a choice of solving for either ΔxH or ΔyH. I'll choose the latter, first multiplying top and bottom by xH then plugging in the first equation, then eliminating minus signs from each side (I hate minus signs):
(ΔyH yH + Δx xH) (xH ‒ xS) yS =
(yS ΔyH + xS Δx) (yH ‒ yS) xH.
Good: this is one equation and one unknown, so it's simple algebra.
(ΔyH yH + Δx xH) (xH ‒ xS) yS ‒
(yS ΔyH + xS Δx) (yH ‒ yS) xH = 0.
Now collect terms in ΔyH and Δx:
ΔyH yS [yH (xH ‒ xS) ‒ xH (yH ‒ yS)] =
Δx xH [xS (yH ‒ yS) ‒ yS (xH ‒ xS)].
Some of those terms cancel! (If I'd had my eyes open I'd have noticed this sooner!)
ΔyH yS (xH yS ‒ yH xS) =
Δx xH [xS yH ‒ yS xH].
Then the bracketed terms differ only in sign:
ΔyH yS = ‒Δx xH
Or, simply enough:
ΔyH = ‒Δx xH / yS.
So using my parameters, I want to move my handlebars up 74.7% the amount I moved the seat back (again, in x-y coordinates: I need to adjust for head tube and seat tube angles).
It's then simple to solve for ΔxH:
ΔxH = Δx yH / yS,
which for my coordinates yields ΔxH / Δx = 76.5%.
So in summary, if I move my seat back 1 cm, I would also want to move it down 2.7 mm. I'd then want to move my bars up 7.5 mm and back 7.7 mm.
But I'm not quite done yet... Suppose my seat angle and head tube angle are both 74 degrees. This is what I measured from the photo (obviously a fairly crude measurement) and I don't recall the dimensions of the Fuji. Okay -- finally time for some trig. I then need to move the post down by 2.7 mm / sin 74° = 3 mm, then move the saddle back on the rails by 1 cm + 2.7 mm / tan 74° = 11 mm. Similarly, with the handlebars, I'd need to add 7.5 mm / sin 74° = 8 mm of spacers to the handlebar. And I'd ideally decrease my stem length by 7.7 mm ‒ 7,5 mm / tan 74° = 5.5 mm.
It might be tough getting the 5 mm shorter stem. But I can also get a stem of the same length and a different angle to bring the bars up and closer. I'll leave it here, though. The main point is a simple shift back on the saddle, to be properly evaluated, requires changes to both coordinates of both primary contact points.

Comments