transmission of road vibration through bike tires (2)
Last time, I analyzed a single bike tire, then assumed that tire suspended half the bicycle mass. This is equivalent to assuming the bike goes over a bump which hits each tire simultaneously, raising and lowering the bike as a unit. The result was an oscillation frequency around 10 Hz (depending on mass and tire pressure).
Well, it turns out this sort of thing has been measured before. Champoux used a bike with accelerometers attached, either riding on a treadmill with a bump attached, or riding outdoors and letting the cracks on the road provide the bumps. He did further experiments with shakers attached either to the front hub, or to the hub and handlebars.
Champoux on his treadmill (from his paper)
When this sort of thing is done, unless damping is extreme, you tend to see oscillations occur at near the normal oscillatory modes of the system. For example, one mode is the one I analyzed: the bike bounces up and down on its two tires together. But Champoux identified a number of modes:
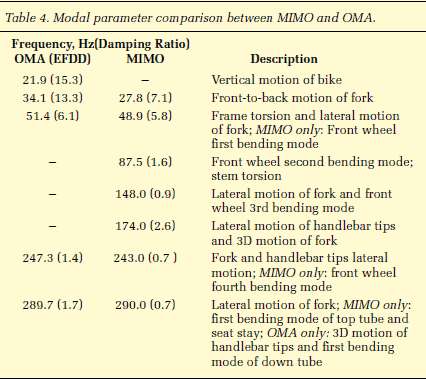Vibrational modes measured by Champoux. OMA: measured while riding on a treadmill; MIMO: measured with shakers on the front dropout and handlebars.
I'll deal more with this table next time. But the thing to observe here is that the "vertical motion of rider and bike" mode is at 21.9 Hz. Hey! I calculated 10 Hz for this. What's up with that? When I saw this table I was deeply disturbed for awhile. Until I figured out the problem. (Thanks to Kraig Willett for the hint).
The problem is, of course, that when the bike hits a bump both wheels don't respond together. The bump hits first the front wheel, which bounces, then the rear wheel, which bounces. At first I assumed these would respond the same as if both were hit together. But these are not uncoupled oscillators. They're coupled by the bicycle frame.
And when you have coupled oscillators you can have multiple oscillator modes. With two identical oscillators (not a terrible approximation) you can have an even mode (which I analyzed in this case) and an odd mode. The odd mode in this case is where the front wheel goes up by a certain amount, and the rear wheel goes down by the same amount. A real hit will be some combination of the odd and even mode, getting a bit of each. But for the standpoint of reducing the high frequency components, the vibrational mode with the higher natural frequency will tend to be the limiting factor.
bicycle oscillation modes
Any sort of oscillation can be considered as a sharing of energy between two reservoirs. For a sping-mass system, you have potential energy (when the spring is fully stretched or compressed), versus kinetic energy (when the spring is in its neutral position, but the object is moving at maximum speed). Each energy varies with time, but the sum is constant (for an undamped oscillator) or decreases smoothly over time (for a damped oscillator). As long as damping is modest, you can get a nice estimate of the oscillation frequency by neglecting the damping.
So consider two cases: (1) both wheels vibrate between ±h, and (2) the front wheel vibrates between ±h while the rear wheel vibrates between ∓ h (opposite sign). In the first case, the bike's center of mass moves back-and-forth, but there is no rotation. In the second case, assuming the bike is symmetric (not too bad an approximation for a bike with equal sized wheels) the center of mass is stationary, but the bike + rider rotates about the center of mass. In the first case, the kinetic energy is determined by the net mass of the system: that's the inertia term. But in the second case, the relevant inertia term is the moment of inertia, which depends on how far mass is located from the center-of-mass. If all the mass is at the center-of-mass, then the moment of inertia is zero.
So the result is that the two modes will have different oscillation frequencies. Consider a simple case: the mass is uniformly distributed in a line segment between the two axles. Then the oscillation frequency will be 73% higher in the odd mode than in the even mode. This is most of the difference between my estimate and Champoux's measurement. In reality, mass is likely clumped a bit closer to the center of mass than this.
Consider another approximation: the human body is a sphere of mass 56 kg, of the same density of sea water (around 1 kg / liter) and the bike has a wheelbase of 1 meter. The radius of the sphere is then around 23.7 cm. Then I add in the bike, which is the line segment I just mentioned, and weighs 6.9 kg (the UCI limit). If I did the calculation right, a very big if, this would result in the odd mode having a natural frequency 5.2 times larger than the even mode.
Reality is obviously somewhere in between. Given this, the factor of two difference with Champoux seems quite reasonable. And even though he failed to identify his "bouncing on the tires" mode as an odd (versus an even) mode, I've got to believe that's what it was.
So to summarize: around 20 Hz.
Next time I'll consider one of those other modes.
Well, it turns out this sort of thing has been measured before. Champoux used a bike with accelerometers attached, either riding on a treadmill with a bump attached, or riding outdoors and letting the cracks on the road provide the bumps. He did further experiments with shakers attached either to the front hub, or to the hub and handlebars.
When this sort of thing is done, unless damping is extreme, you tend to see oscillations occur at near the normal oscillatory modes of the system. For example, one mode is the one I analyzed: the bike bounces up and down on its two tires together. But Champoux identified a number of modes:
Vibrational modes measured by Champoux. OMA: measured while riding on a treadmill; MIMO: measured with shakers on the front dropout and handlebars.I'll deal more with this table next time. But the thing to observe here is that the "vertical motion of rider and bike" mode is at 21.9 Hz. Hey! I calculated 10 Hz for this. What's up with that? When I saw this table I was deeply disturbed for awhile. Until I figured out the problem. (Thanks to Kraig Willett for the hint).
The problem is, of course, that when the bike hits a bump both wheels don't respond together. The bump hits first the front wheel, which bounces, then the rear wheel, which bounces. At first I assumed these would respond the same as if both were hit together. But these are not uncoupled oscillators. They're coupled by the bicycle frame.
And when you have coupled oscillators you can have multiple oscillator modes. With two identical oscillators (not a terrible approximation) you can have an even mode (which I analyzed in this case) and an odd mode. The odd mode in this case is where the front wheel goes up by a certain amount, and the rear wheel goes down by the same amount. A real hit will be some combination of the odd and even mode, getting a bit of each. But for the standpoint of reducing the high frequency components, the vibrational mode with the higher natural frequency will tend to be the limiting factor.
Any sort of oscillation can be considered as a sharing of energy between two reservoirs. For a sping-mass system, you have potential energy (when the spring is fully stretched or compressed), versus kinetic energy (when the spring is in its neutral position, but the object is moving at maximum speed). Each energy varies with time, but the sum is constant (for an undamped oscillator) or decreases smoothly over time (for a damped oscillator). As long as damping is modest, you can get a nice estimate of the oscillation frequency by neglecting the damping.
So consider two cases: (1) both wheels vibrate between ±h, and (2) the front wheel vibrates between ±h while the rear wheel vibrates between ∓ h (opposite sign). In the first case, the bike's center of mass moves back-and-forth, but there is no rotation. In the second case, assuming the bike is symmetric (not too bad an approximation for a bike with equal sized wheels) the center of mass is stationary, but the bike + rider rotates about the center of mass. In the first case, the kinetic energy is determined by the net mass of the system: that's the inertia term. But in the second case, the relevant inertia term is the moment of inertia, which depends on how far mass is located from the center-of-mass. If all the mass is at the center-of-mass, then the moment of inertia is zero.
So the result is that the two modes will have different oscillation frequencies. Consider a simple case: the mass is uniformly distributed in a line segment between the two axles. Then the oscillation frequency will be 73% higher in the odd mode than in the even mode. This is most of the difference between my estimate and Champoux's measurement. In reality, mass is likely clumped a bit closer to the center of mass than this.
Consider another approximation: the human body is a sphere of mass 56 kg, of the same density of sea water (around 1 kg / liter) and the bike has a wheelbase of 1 meter. The radius of the sphere is then around 23.7 cm. Then I add in the bike, which is the line segment I just mentioned, and weighs 6.9 kg (the UCI limit). If I did the calculation right, a very big if, this would result in the odd mode having a natural frequency 5.2 times larger than the even mode.
Reality is obviously somewhere in between. Given this, the factor of two difference with Champoux seems quite reasonable. And even though he failed to identify his "bouncing on the tires" mode as an odd (versus an even) mode, I've got to believe that's what it was.
So to summarize: around 20 Hz.
Next time I'll consider one of those other modes.
Comments
Tires are unsprung masses that filter high frequency, low amplitude vibrations. I have read the study you quoted before and even made a mention of Velus' research work on my blog in the past, including some bits on EMA.
Some personal observations :
1) Difference in EMA between no cyclist vs occupied cyclist, as the latter introduces vibration at the handlebars. Still, the numbers behind the modes in EMA (SIMO) are sort of close to what would be seen in a modern sporting motorcycle, you know..for example, with a mass of 190 kg, 1st through 4th modes are 23, 28, 32 and 36 Hz respectively although structural elements and their planes of vibration differ. Your calculation of 10 Hz sounds a little low-ish to me.
2) OMA results in fewer modes than that seen in the EMA in the lab but perhaps this is from the fact that they exaggerated the treadmill bump and hence the excitation made available. I have written about the dynamic behavior of the bicycle, and in Part II of my series, I noted that the state-of-the-art mathematical model designed for the bicycle at Delft has about 24 degrees of freedom (DOF=independant co-ordinates). It is ridiculously complex than previously imagined. This may mean that the bicycle actually shows 20+ different modes of vibration as # of vibration modes should equal the DOF. I don't think it is practical to study all these little tiny modes, there's more sense in concentrating on the dominant ones that affect dynamic comfort.
3) In the past I have rummaged through available literature to find an objective set of absolute limits for vibration. I have found zero for the bicycle but some for the passenger car. SAE's Janeway Report for amplitude vs frequency is a good resource to have and is often quoted in vibration literature but I find that you cannot fix the limits for human comfort objectively. The problem is complicated by variations in individual sensitivity and diversity of test method and by the fact that such "limits" are based on just single sinusoidal frequencies.
4) I have thought a lot about vibration dampening of tires and it is almost a forbidding topic, specifically due to the math involved in handling the degrees of freedom and the modeling parameters. Computer programming and analysis is apt. Experimental measurements are even better.
Measurement of vibration in Museeuw's flax bike.
Nice work! I'm going to be looking your posts over carefully. I think my calculation for the even mode is good (hard to believe I made a factor of four error in the spring constant of tires). Clearly the odd mode is more relevant to single-wheel events, and the odd mode frequency comes out a bit right. Maybe I'll take a stab at estimating my moment of inertia, which will allow me to estimate the odd mode frequency more precisely than assuming I'm a sphere of sea water.
I am also a cyclist who tries to understand the transmission of road vibrations to saddle and handlebar. I agree that it is complex subject, so joint brain power may do some good.
You seem to be unaware of two studies that contain interesting data.
One is from 1993, in German: http://www.forschungsbuero.de/PV38_S6_8.pdf . It confirms that the resonance frequency of wheels is in the range of 7-10 Hz, at 5 bar inflation pressure and a load of about 60 kg (not mentioned in this article, but in the original study by Kai Moennich). There are also some estimates of the damping coefficient.
The second is a recent master thesis from the University of Ghent. It is one of a series of investigations around the Museeuw bike: http://buck.ugent.be/fulltxt/RUG01/001/805/380/RUG01-001805380_2012_0001_AC.pdf . I haven't yet found a clear result that delineates the effect of the flax-composite frame, but it describes a lot of effects from the tires and the wheels. A pity that the author didn't truncate his data to a few significant digits, but the report is a treasure trove for serious study.
It is interesting that the difference in the numerical model between the primary and secondary modes is 69%, where my stick model (modeling the bike as a stick connecting the hubs) yielded 73%. It goes to show the utility of simple models.