Estimating effect of the wind on run speed @ CIM 2012
The big factor I've not addressed in the conditions at CIM was the wind. There was a strong wind from the south, and the route finished further south than it began. It was fairly W-to-E or N-to-S at all time, moving along orthogonal trajectories. The latitudes reported by my Edge 500 extended from 38.564 degrees to 38.704 degrees, a difference of 0.140 degrees, which at 90 degrees per 10 million meters yields 15.51 km north-to-south out of the 42.2 km race.
So the question is, given the conditions of the race, how much time is added by running 15.51 km of the course into a block head-wind? I assume a side-wind had no effect.
Weather reports of wind are generally typical of 10 meter elevation, and I extend only from 0 to 1.70 meters (in shoes). Approaching ground level, wind speed is reduced. An analytic approximation to this effect which I have used before is the Hellman formula:
vw = vw0 ( h / 10 meters )α
Assuming all increments in height have essentially equal Cd dA, I can integrate wind resistance over height to yield:
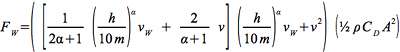
I checked this integral numerically and it matches. In any case, you can see it has the correct behavior for α = 0 (constant wind all the way to the ground) in which case it reduces to the usual formula (force proportional to the square of the sum of runner speed and headwind), and in the case α infinite (no wind below the reference altitude) in which case you get the still-air wind resistance.
All that remains is to find values for the constants. For the Hellman constant, I have used 0.34, which is applicable to "neutral air above human inhabited areas", but here I'll use 0.27, which applies to "unstable air above human inhabited areas." I'm not sure what "unstable" means, but it seems the gusting winds we encountered were fairly unstable.
For wind speed, I checked the portion of the run over the course where most of the north-to-south progress was made, first getting the times from my Strava activity, then looking up the wind speeds on Weather Underground using the historical data for Fair Oaks, which was at the southern end of the first of two north-to-south portion. Although the wind gusted to 49 mph with 32 mph sustained at the time of the race start, I was going south from approximately 7:42 to approximately 9:00, and during this period the average wind speed was 11.7 mph = 5.21 m/sec. Sure, there were gusts to up to 52 mph, but I'm going by average. I take these winds to apply to 10 meter elevation, as is typical.
For air density, I go by the reported temperature of 55 F (13C) and the pressure of 29.7 inches of Hg. I was able to convert that to the units I want, which is 1.233 kg/m3.
I estimated CD = 1 (since my clothing was relatively floppy) and A = 0.4 m wide by 1.7 meters tall = 0.68 meters squared.
For running speed, I used my average speed when heading due south, which was 3.54 m/sec.
The net result is 0.857 newtons of retarding force. This is in contrast to the still air retarding force of Fw = 0.525 newtons. So how is this possible? The headwind is changing the wind resistance by only 63%. The answer is the Hellman formula: wind sheer results in a substantial reduction of wind speed over much of my height. Even if I feel a wind in my face, there's less wind at my belly button, and less still at my knees.

focus on zero-grade point = 3.4 kJ/kg/km
If I assume a marginal metabolic efficiency of 25%, and I can integrate this additional force of 0.332 newtons over the 15.51 km of north-to-south running to come up with a total metabolic cost of 20.60 kJ of metabolic cost added by the headwind. This is out of a total metabolic cost in the marathon of approximately (3.4 kJ / kg / km) × 59 kg * 42.2 km = 8465 kJ. The conclusion is the net loss of speed is 0.248% over the whole marathon, 0.66% during the portions where I was running southward. That's around 31 seconds.
You might argue this is a low-ball estimate because it assumes a constant wind speed, while the actual wind was gusting, and since wind force is proportional to the square of the relative wind speed the effect of gusting wind will be greater than that of the effect of constant wind at the same average. On the other hand, this analysis fails to consider drafting, as I tried to run behind others during these segments.
So I decided to look at the data. For the first 17 km, before I slowed, I extracted my heading (1 = north, -1 = south) and extracted my speed, applying 30-second smoothing to each. I plotted these and did a regression, as follows:

The result is that speed when I was running due south was approximately 1.25% slower than when running perpendicular to the wind, and my overall pace was reduced by 0.58% versus what the regression predicts for running perpendicular to the wind. I admit this is far from the most compelling regression I've ever seen, but while these numbers are well above the prediction I got from the documented wind speed with the other estimated values, they are still well shy of the 3.7% reduction in runner speed I derived relative to last year.

Grade versus heading to compensate for effect of grade difference going south then west and north
I can do a bit better than this by correcting for correlations between road grade and heading. If I do the same sort of regression for road grade on the course, I find the dependence of road grade on heading is 0.31%, so on average the southern legs averaged a 0.31% more downhill than the cross-wind sections. This compensates some of the headwind effect. From Minetti's data I see each 1% change in grade changes the metabolic cost of running by approximately 0.2 kJ/kg/km near zero-grade, so this difference in grade has an effect of 0.062 kJ/kg/km, or 1.82% of the baseline 3.4 J/kg/km metabolic cost. So you'd expect the southern legs would be faster due to being more downhill, but in fact they were slower. You could then argue the net effect of the wind wasn't 1.25%, but rather 3.07%. Still, amortizing this over the full length of the marathon yields a net slow-down of 1.11%, which is 2:10 applied to my pace here of 3:16/marathon. 1.11% is still well below the 3.7% derived number.
You could argue this discrepancy is because I am assuming constant effort, and that runners tried harder on the southern sections attempting to keep their target pace, and they thus paid a price for the headwind not only on the southern legs, but additionally on the western legs which followed due to increased fatigue. This is quite plausible, but I cannot easily assess it.
So in summary, I approximated the effect of wind resistance assuming steady wind and no drafting and the Hellman formula for ground shear got a relatively small effect. This analysis neglected wind gusts and drafting, the first expected to yield bigger effect, the second less effect. I then empirically looked at my speed during the first 29 km (before I slowed) and saw the southern sections were indeed slower, but only by 1.25%. However, these sections were also more downhill, so you'd expect them to be faster, not slower, and taking the net wind effect after subtracting the grade effect yields 3.07%. The effect over the full marathon would be expected to be 1.11%, which is significant but still less than the observed difference.

Comments