Converting Run Times to Cycling Times for Low-Key Hillclimbs Part 5: Eccentric stress

A weakness with the approach described so far is that it over-estimates speeds on downhills, as Minetti documented himself in his paper. His data were from mountain races, the focus of the work (test subjects were elite mountain runners), so technical issues play a role, for example not wanting to slip on gravel, while for Low-Key Hillclimbs most descents are on paved roads or, in the case of a few short descents on Kennedy this year, on smooth fire road. But there is another factor on descents in addition to risk of falling: the eccentric pounding on leg muscles contributes to a trauma not directly reflected in rate of oxygen consumption (the metabolic metric used by Minetti). Therefore I think it is beneficial to introduce a heuristic stress component related to running downhill.

It would be tempting to add a speed limit similar to what I applied to cycling. But running uphill is clearly less stress than running down. So while a speed limit might pragmatically approach the desired goal, it's less physically based. It seems the trauma is more related to VAM, or the rate of vertical ascent. Clearly this is not linearly dependent on VAM, since in the limit of positive VAM there is no eccentric loading, while in the negative VAM direction the eccentric loading should increase without limit. So I need some sort of nonlinearity which has this character.

Then the issue is for negative VAM how the stress relates to VAM in the large negative limit. It could for example be proportional to negative VAM, or proportional to its square. Negative VAM represents a rate of potential energy loss which must be absorbed by the legs. Since the rate of change of potential energy is a measure of power, and since metabolic activity is also power, it makes sense that there would be a linear relationship.

So then the question is how to model this effect using VAM. It would be tempting to simply count negative VAMS but ignore positive ones. But when I run on the flat, the nature of running is my legs are absorbing impact with every foot fall. When I'm trudging up a steep slope, there is much less such impact. So there should be a difference not only between negative VAMs, but to a lesser extent also between zero and slightly positive, or lesser still, between slightly positive and more positive VAMS. So I want something which is linearly dependent on steep negative VAMs but then smoothly approaches zero as VAM crosses into the positive zone.

The remaining question is then if VAM is linearly dependent on negative VAM, what is the effective negative VAM (from a leg trauma point of view) of flat ground. Here lacking any data (I could look up papers, but this is a heuristic model, after all) I need to make a decision based on simple reasoning.

Fortunately, I already did a simple physics-based kinetic analysis of running back in April 2010. There I was trying to estimate optimal cadence, which I concluded was a balance between power raising and lowering center-of-mass (which dominates at low cadence) and raising and lowering feet (which dominates at high cadence). I got the optimal of 95, which is right where I like to run.

I'm not interested in the foot component: the center of mass component is the larger stresser. So that part is:

h = ½ gravity t²

where t is the time between leaving the ground and reaching maximum height. In that analysis, I assumed 70% of the stride time was spent ballistic, and of that, half is spent rising (when running on level ground), so I get t = 35% of the stride time, or 0.1105 seconds. This results in center of mass rising 6 cm each foot stroke. Lateral motion is 132 cm. So this is an average each time I go laterally 132 cm I need to absorb 6 cm of potential energy loss. That's equivalent to an effective grade of -4.55% (using sine, not tangent).

I then need to relate this effective grade for eccentric impacts to the actual road grade. In the negative grade limit the effective grade is simply the grade itself. For zero we have the answer. For positive grade where I'm trudging uphill the grade shouls approach zero. I like the following equation for this sort of thing, since it has application in semiconductor physics, and has the correct behavior. I use g' to refer to the sine of the angle, instead of the tangent which is the formal definition of grade (here I'm more interested in altitude change per distance traveled, not altitude change versus map distance):

g'_eff = g'₀ ln | 1 + exp[g' / g'₀] | ,

where g'_eff is proportional to the eccentric component of work for a given speed, and g₀ is the effective grade for zero slope for the purpose of eccentric force trauma (and is negative).

The aerobic cost of eccentric work is already captured in Minetti's measurements, so I need to consider here only the trauma component. A similar question is: if I were to pound your legs with a hammer, even if your heart rate was unaffected, how much would this slow you down? I need to decide for every unit of eccentric work, what fraction of that is subtracted from the total aerobic capacity (not just the propulsive aerobic capacity)?

Rather than find scientific justification in a choice for this, I will declare it to be a fitting parameter. Note the coefficient relates potential energy to metabolic heat, so there is an implicit metabolic efficiency component.

The metabolic rate (per time) will be proportional to speed, so the metabolic rate per distance will be speed-independent, since time and distance are related by speed. The equation then becomes:

Δ(dH/ds) = -K_x gravity g'₀ ln | 1 + exp[g' / g'₀] |,

where K_x is the empirical coefficient (the "x" is for "eccentric") and dH/ds is the effective total metabolic cost of running (per unit mass, inversely proportional to speed). This is not an actual metabolic cost, but rather the total cost in terms of a fixed available sustainable rate.

After including this term, I then need to renormalize to restore my target flat-ground pace.

There is one fitting parameter in this model and that's K_x. There's no universal value for this different runners have different styles and can handle different muscular loads differently. So I just tried K_x = 1, and here's what I got:

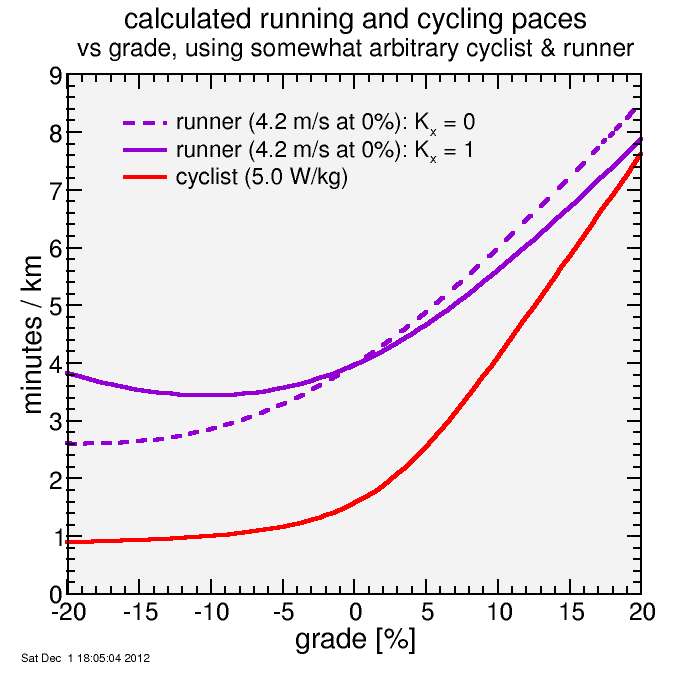
calculated minutes per km for model cyclist and runner. For the runner, I tried two values for the coefficient for the effect of trauma on the "cost" of running (in addition to aerobic metabolism, which is all that was considered previously). The pace at zero grade was fixed at 4.2 m/s. With K_x = 1, the peak speed descending is at close to -10% grade.

You can see in the plot that the effect of modeling the trauma of running downhill has substantially reduced the speed for negative grades, and somewhat reduced the speed difference between zero grade and uphill running. The most notable feature of the new model is the maximim in speed which now occurs at near -10% instead of closer to -20%. This is consistent with my experience: for roads in the -20% range, which I encounter every time I run to the train in the morning, I need to substantially limit my pace below the aerobic limit. So I view these results as plausible pending further experimental data.

The effect of this on the score adjustment versus grade is shown here:

Score adjustment versus grade with the revised model.

Here is the revised scoring adjustements as would be applied to the climbs used in the 2012 Low-Key Hillclimb series:

fn	trun	tbike	ratio	score factor
1	2649	1612	0.6085	1.28
2	1734	1237	0.7136	1.092
3	2443	1362	0.5576	1.397
4	6110	2847	0.4659	1.672
5	6941	3310	0.4769	1.634
6	2814	1844	0.6553	1.189
7	2071	1447	0.6986	1.115
8	9093	4651	0.5115	1.523

Applying these to Matt Allie's scores from the season make gives him 105 for week 2 (Quimby Road) and 96 for week 8 (Mt Hamilton Road). This brings them a bit closer together then they were before I applied the model enhancement.