using the analytic running-mass model

It's always risky to use analytic models I develop here in follow-up posts because I have too great a rate of changing my mind about analytic models, and in these cases I face the prospect of revising not only the model but also subsequent posts relying on the models, and these dependencies are not tracked. But I'll boldly forge ahead here.

Note already my model is suspicious because it predicted a substantially higher dependence on shoe mass than what is reported from experimental measurements, so interpret these conclusions with caution.

First, I'll look at the cadence dependence of the different energy components:

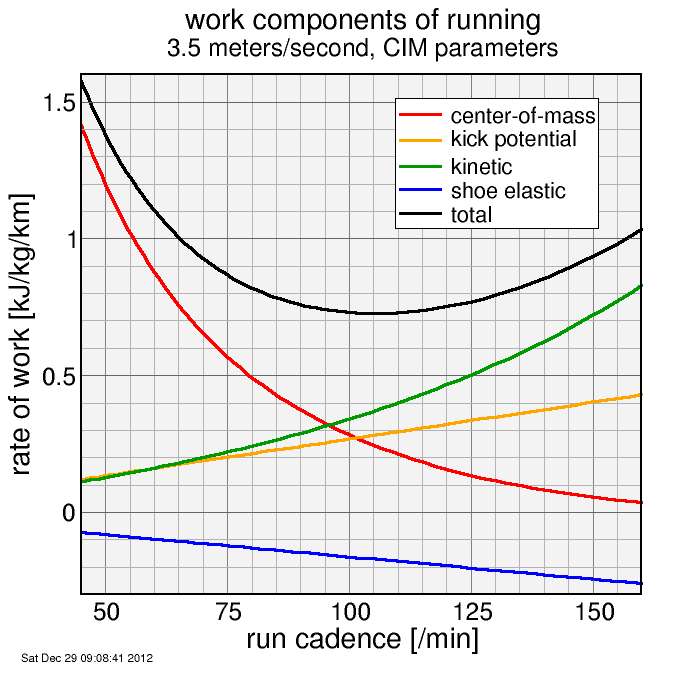
Force versus cadence

The potential energy component associated with bouncing the center-of-mass dominates at low cadence. As the cadence increases, two other contributions increase in importance: the potential energy of kicking the foot up, the the kinetic energy of swinging the foot forward. Additionally, the faster the cadence the more energy return from the elastic storage in the shoe. With increasing cadence the total power decreases, hits a minimum, then increases. The optimal cadence with these parameters is near 105/minute, although given the crudeness of parameter estimates I would place little faith in the precision of this estimate.

An interesting aspect of this model is how speed depends on the total mass versus how it depends on the foot mass. I derived d ln P / d ln M, which is the fractional change in power or retarding force associated with a fractional change in total mass, assuming the change in mass is inert mass (as opposed to mass below the knees, according to the assumption of my model). I have often in the past assumed this value was 1: that a 1% change in total mass results in a 1% change in speed, and I have seen this assumption used elsewhere. But my model shows that higher the running cadence, the lower this dependence on total mass, and near the optimum cadence (105/min with these model parameters) it's 1/3.

fractional dependence on total mass, assuming additional mass is inert

Inert mass has the least effect, but mass on the foot (according to the model) has the greatest effect. I show this in a slightly different way, as % change in power or force per 100 gram change in shoe mass (each shoe). The reason for this is % change in total mass has obvious meaning, but % change in shoe mass is less relevant.

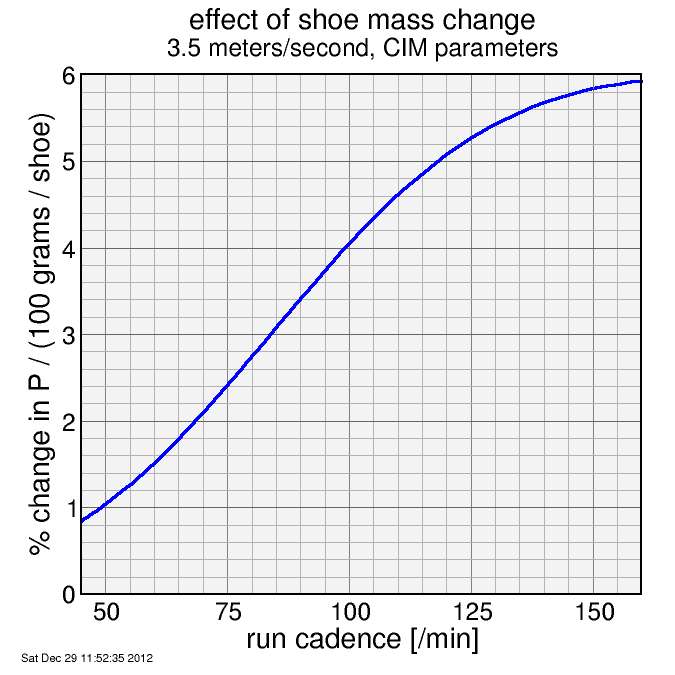
fractional on power from given change in shoe mass

This paper by Franz, et al. claims a 100 gram increase in shoe mass increases the metabolic cost of running by 1%. My plot suggests this might be true, for the assumed model parameters, for unrealistically low running cadences (60/minute), but for more typical cadences in the 80-95 range the effect of shoe mass is greater: more than 3%.

So in summary, the model predicts an optimal cadence of around 105/minute. This involves trading off two processes which had an increased energy cost with higher cadence (kinetic energy of dragging the foot forward + potential energy of raising the foot) and two processes which result in less energy with higher cadence (the raising of the center-of-mass and the return of energy from the shoe). Since only the center-of-mass component depends on inert mass, the effect of a 1% increase in total mass via an increase in inert mass can be substantially less than 1% (for example, 0.5% at a cadence of 90/minute). On the other hand, the model predicts shoe mass can be much more important: for example a 100 gram increase in shoe mass ( 0.34% of total mass, counting both feet ) can increase the power requirements by 3.8% at a cadence of 90/minute.