effect of gusting vs steady wind on running wind resistance @ CIM

One limitation of my analysis of wind in CIM was my assumption of uniform wind speed. It isn't hard to investigate how gusting wind would affect the result, however. While the actual time-dependence of wind is complex, a simplistic assumption can at least establish the bounds for what uncertainy exists.

So I make a small perturbation to the assumption of uniform wind speed. Instead, I assume the wind is either zero, or a non-zero "gusting" value which is some multiple k of the average. Since the average is fixed, the wind is zero for a fraction of the time (1 - 1/k), and it is gusting for a fraction 1/k.

So with the same derived average wind speed, I changed the constant k. As before, I assume the wind speed is characteristic of a 10 meter elevation above ground level. I assumed the Hellman formula for the reduction in wind speed as a function of position closer to the ground. I then integrated wind resistance over my height in shoes (170 cm).

Before showing results, it's worth thinking about what to expect. The resistance force from wind per unit height is assumed proportional to the square of the relative wind at that height, so proportional to (v + v_w)², where v is the runner speed and v_w is the wind speed athat position z above the ground.

If v_w is smaller than v, it is useful to transform this to v² [ 1 + (v_w / v)]², which can be expanded to v² [ 1 + 2 v_w / v + (v_w / v)^{2 ].}

At zero wind speed, this term is simply v². If I assume v_w0 is the average wind speed, then if I define k = v_w / v_w0 during gusts then the term becomes v² [ 1 + 2 k v_w0 / v + k² ( v_w0 / v )² ].

I am interested in the average between the gusting and zero-wind times. This average is:

(1 - 1/k) v² + 1/k v² [ 1 + 2 k v_w0 / v + k² ( v_w0 / v )² ]

I can simplify this:

v² [ 1 + 2 (v_w0 / v) + k (v_w0 / v)² ]

or perhaps I can write it:

v [ v + 2 v_w0 ] [ 1 + k (v_w0 / v)² / (1 + 2 v_w0 / v) ]

So the result is a constant value plus a fractional proportionality constant proportional (for small wind speed) to the square of the ratio of the wind speed to the runner speed. At higher wind speeds this becomes proportional to the ratio of wind to runner speed rather than the square of the ratio.

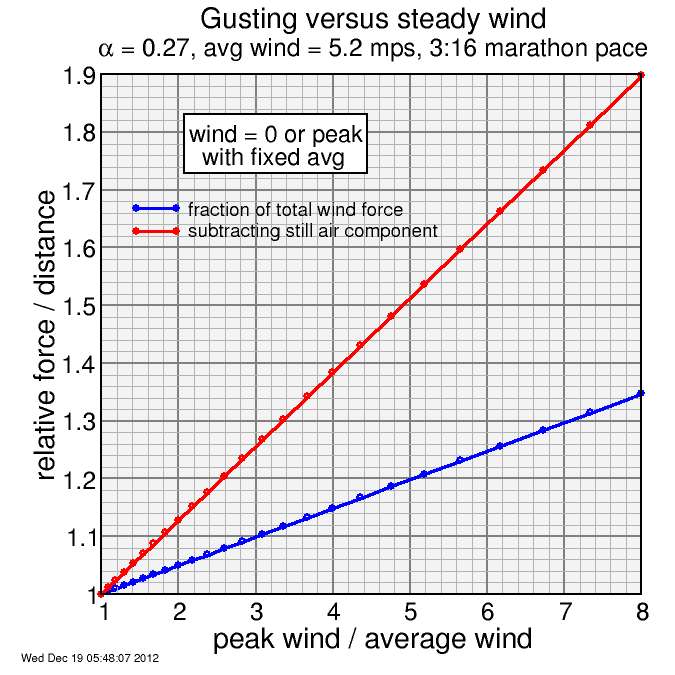
So here's what I get when I run the numbers. I plot only the fractional effect, not the force in Newtons.

First, the analytic calculation is mirred in the numerical result: there is an intercept with a linear dependence on k.

The plot shows two curves. One (blue) is the total wind resistance, including the effect of the runner's speed, versus the constant-wind-speed case. This has a relatively gradual slope. Analytically I can write this curve:

1 + (k - 1) v_w0² / (v + v_w0)²

The other curve subtracts off the wind resistance the runner would experience in still air. This simplifies down to the following:

1 + (k - 1) v_w0 / (2 v + v_w0)

This is proportional to the total energy cost per distance of the wind itself.

For hurricane-level gusts there's at least a 65% error in effect of the blowing wind (red curve), but for the approximate factor of 3 between the reported wind gust speed and the average speed, the average force increment is only 25%. So it seems, if I trust the average wind speed data from the weather station in Fair Oaks, the assumption of constant wind speed was not a terrible one in this instance. The key here is the Hellman formula which reduces the wind speed at runner level.

As long as the wind direction is constant, this is the "worst-case" assumption for a given wind gust speed. Real-life wind patterns with a given peak speed and a given average speed will have a lower multiplier.