Converting Run Times to Cycling Times for Low-Key Hillclimbs: Part 4

Last time I derived a score conversion curve for running versus cycling for roads of constant road grade. This time I apply that curve to real road profiles on a detailed basis.

First I need to select the roads. Good examples from the 2012 Low-Key series are Quimby Road and Mount Hamilton Road, each run by Matt Allie. While these climbs differ substantially in their endurance component, something not addressed in this model, they also differ substantially in road grade, with Quimby being much steeper than Hamilton, the latter including even extended descending sections. Matt scored 96 and 63 points in the two climbs, respectfully, so if the ratio of the score conversion factors is the same as the ratio of these scores, it suggests (if he ran equally well) that the approach is on track.

Here again is the plot of conversion factors versus grade:

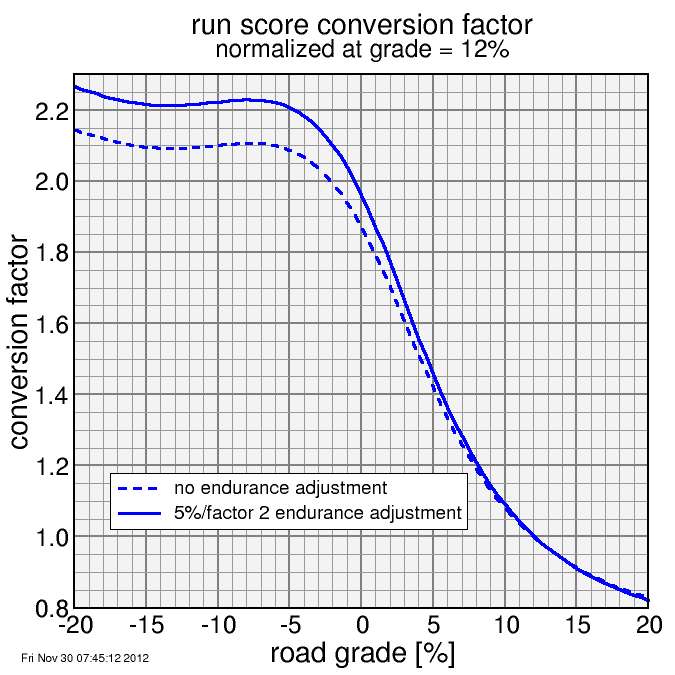
Grade plots for the two climbs are as follows. The smoothing in these plots is a bit different than I use in the algorithm, but they are highly representative:

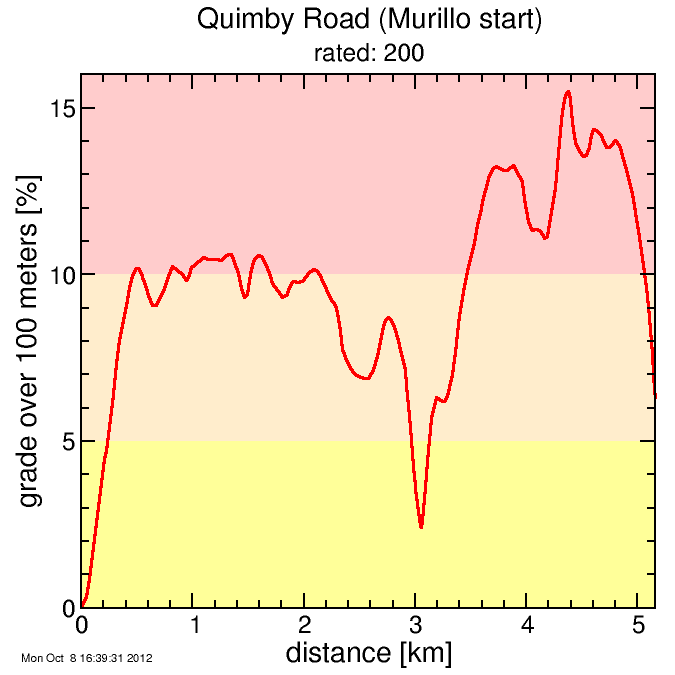
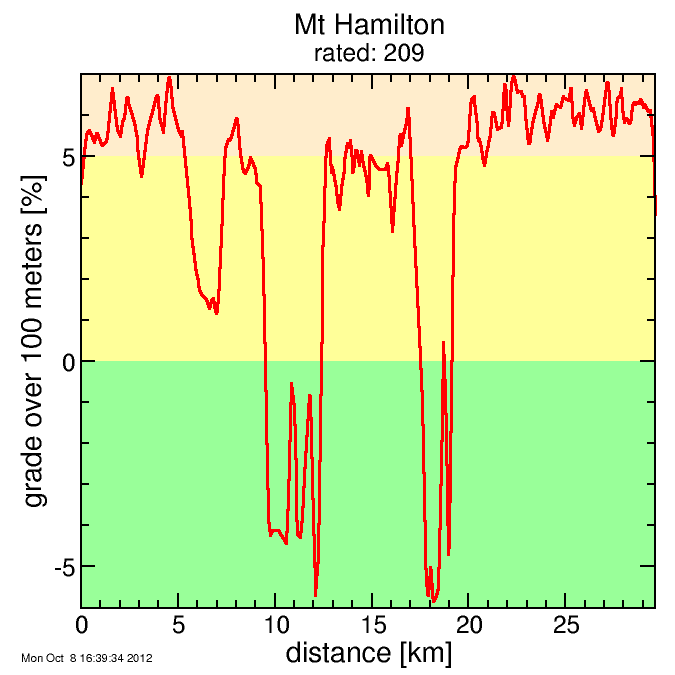
You can see Quimby sustains up around 14% for a significant portion while Hamilton barely cracks 6%, and even includes descents at 4% and 6%. So the striking contrast of this comparison presents an excellent test of the algorithm.

I coded up the algorithm and ran it on last year's climbs. This is the result:

week	trun	tbike	ratio	score factor
1	2808	1612	0.5741	1.262
2	1851	1237	0.6682	1.084
3	2562	1362	0.5318	1.362
4	6307	2847	0.4514	1.605
5	7154	3310	0.4628	1.565
6	3007	1844	0.6134	1.181
7	2195	1447	0.6593	1.099
8	9446	4651	0.4924	1.471

If I apply the factors for Quimby (week 2) and Hamilton (week 8) to Matt's scores of 96 and 63 points I get 104 points for Quimby and 93 points for Mt Hamilton. The difference had dropped substantially, however, from 52% more for Quimby to 12% more for Quimby, so I managed to eliminate around 77% of the difference. An interesting factor with Mt. Hamilton is its extended descents. Indeed Minetti in his paper reports that his measurements overestimate the speed at which runners can descend, because issues other than metabolic cost tend to become speed-limiting.

Then I have my scores. I scored 84 on Quimby (week 2) and 45 on West Highway 9 (week 4). Applying the correction factors yield 91 for Quimby and 72 on West Highway 9. My 2012 scores differed by 72%, while with the proposed scheme the scores would have differed by 27%, so I managed to eliminate 2/3 of the difference.

So in both cases the steeper climb remained the higher scoring one. But there's no fitting parameters in my model: I take Minetti's measured metabolic costs as inversely proportional to speed after making the small adjustment for wind resistance, so it is what it is. In any case it is clear this will go a long way to making things fairer for runners doing different climbs in 2013.

Next time I'll look at making the model a bit more sophisticated, by including a model for the reduction in aerobic power which likely occurs when descending steep roads.