height of effective wind speed when running (more post-CIM analysis)

I've been modeling the wind speed as a function of height with the Hellman formula:

v_w = v_w0 ( h / 10 meters )^α

With this dependence, I need to integrate the wind speed over the full height of the body, assuming the effective C_D dA per unit height is the same (in a constant wind, the force per unit height is the same).

I got this result for the total force from the wind resistance:

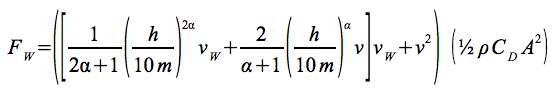
The Hellman formula assumes wind exactly at ground level is zero. Wind speed then increases to the top of the head. Somewhere in between the wind speed is the value which can be applied to the constant wind formula for wind resistance:

F_W = ½ ρ C_D A (v +v_weff)²

Here v_weff is the effective headwind speed. The question I'll ask here is at what fraction of the runner's height does the wind speed equal v_weff?

Consider the case where the wind varies linearly with height, and where the net wind resistance is linearly dependent on the wind speed (for example, the wind speed at human height is a small fraction of the runner's speed). Then you'd expect the wind resistance to be the same from the average wind speed hitting the runner, which is at half his height, assuming all segments of height contribute equally for a given wind speed at that height.

But consider the case, again when resistance is linear with local wind speed and where the wind speed follows Hellman's rule, proportional to height to the α power. If I integrate that over the height, I get 1 / (α + 1) times what I'd get using the wind speed at the top of the head. This value occurs at a relative height 1 / (α + 1)^1/α. So for α=0.27, which is what I used for CIM, I get 41.2% of the runner's height is where the wind speed = the average value, which I assume is the average per-height wind resistance.

If I assume the wind is stronger, and has a nontrivial component proportional to the square of the height. Then the average resistance doesn't come from the average wind speed across the body, but rather the portions where the wind speed is is greater closer to the head will contribute disproportionately. So this will shift the point where the wind speed = v_weff higher.

So in summary: for α = 1, in which case the wind speed is linear with position, I expect for small wind speeds the height at which wind speed = v_weff to start at 50% of height, then increase as wind speed increases. If α is smaller, I expect it to be at a lower height (for example 41.2% of height for α = 0.27), but still increase for higher wind speeds. I calculated the numerical result using parameters I used for me running CIM and here's what I got:

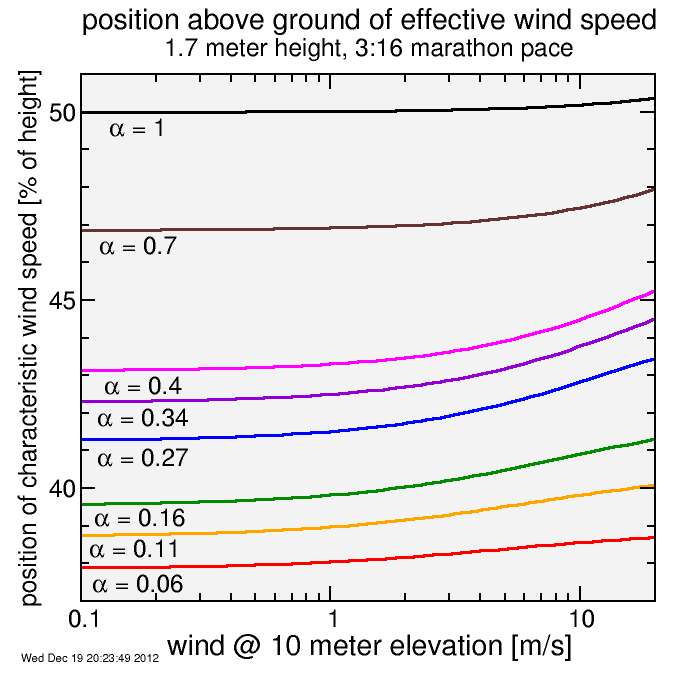
So the answer is for typical conditions the wind between 40-45% of height is the wind producing the per-area wind resistance which would yield the correct total wind resistance for the body. So if you feel wind in your face, that's not the most relevant wind speed, but rather it's the wind closer to your covered bits where I hope you don't feel it.

One interesting observation: in the limit α goes to zero, which is the limit of constant wind, the height of characteristic wind (in the low-wind limit) is the limit as α goes to zero of 1 / (α + 1)^1/α, which you might recognize from calculus as 1/e. That wasn't expected.

One more thing: all of this depends on the Hellman formula being good to very low altitude. There's nothing fundamental about it: it's a heuristic formula. It's unclear that a constant value of α should apply from zero to ten meters. Other functional forms, like exponential, may be more realistic. So don't get hung up on exact results. The important thing is the trends.