Leulliot mass-versus-height for cyclists

After reading Cozy Beehive's review of a recent article, and having read editor/primary contributor Jan Heine's absolutely excellent The Competition Bicycle, I knew I had to subscribe to Bicycle Quarterly. So I jumped straight in: I ordered the past year's worth of back-issues and committed to a 2-year subscription. After having become acclimated to the usual commercial touchy-feely stuff which is the staple of most cycling publications, the analytic approach taken by Bicycle Quarterly is refreshing. Sure, any sort of analysis is going to be flawed in some way, but at least there's something with substance there to bite into. Plenty of stuff for blog posts.

First I checked out the Summer 2010 copy, since this is where the article analyzed by Cozy Beehive was printed. But there's a lot more there than just the analysis of Tour de France speeds. A real gem was a translation of an article from a 1939 Vélo, by Jean Leulliot: How to Become a Bicycle Racer. A lot of good stuff printed there, less different from much of today's advice than one might expect, but I'm attracted to math, and an interesting mathematical contribution was his recommended weight-versus-height formula:

mass = (height ‒ 100 cm) × (1 kg / cm).

These days recommendations are more typically made in terms of BMI:

mass = BMI × height².

So I decided to compare the two. How did Leulliot's formula compare to BMI?

Here's a plot:



You can see his formula results in a higher BMI for taller riders than for shorter riders, at least up to the maximum height plotted of 2 meters (the recommended BMI would begin dropping beyond this, but the recommendations probably weren't intended for such exceptionally tall people).

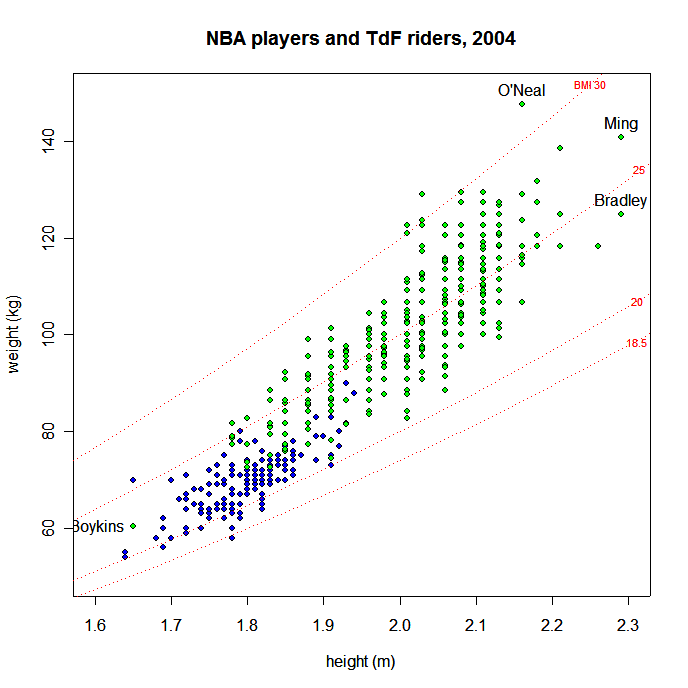
Now this is hardly new. Robert Chung produced the following plot, showing BMI versus cyclists and NBA players (to expand the height range), showing BMI tends to increase with height:



However, there's nothing scientific about the BMI formula: it's heuristic, designed to be easy to calculate by hand. There's no fundamental reason the "2" be an integer. So I fit a curve to the Leulliot formula and got the following adjusted BMI:

mass = BMI' × height^2.38.

Note the two BMI values have different units and so can't be directly compared to each other without establishing a reference height at which the two should agree. But while I won't take the time to plot it, this value does quite a nice job of reproducing the slim side of Chung's plot (I focus on the slim side since basketball players obviously tend towards more upper-body muscle than cyclists).

But here's a plot of Leulliot's formula superposed directly (hand-drawn) on Chung's plot:



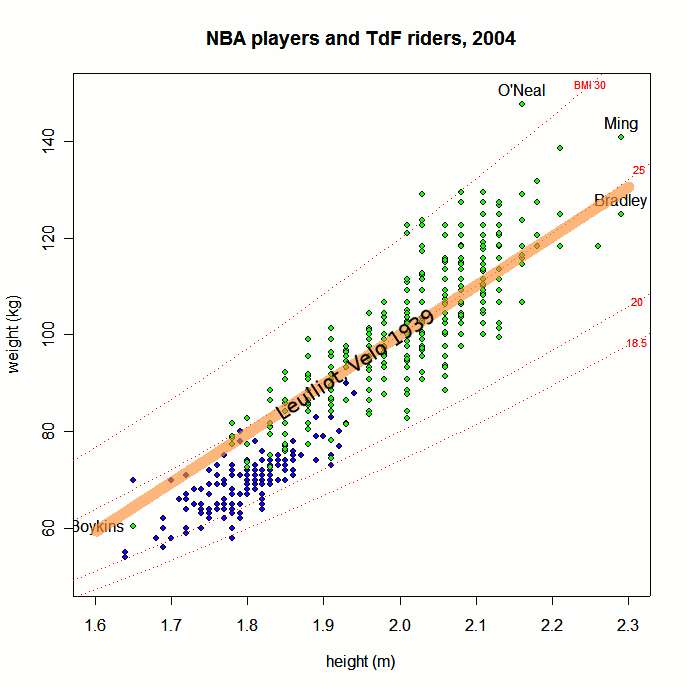
Considering that some of the NBA players are likely too stocky to race the Tour de France, the Leulliot limit line does fairly well, arguably better than the constant BMI target assumption.

The issue with any height-weight formula, of course, is mass depends on body type, not just height. Longer legs and you're probably lighter, long torso and you're probably heavier, both with the same build. So all such formulas are fuzzy. But it is interesting around a mean height of 175 cm, the Leulliot formula seems to come closer to Chung's plot than the more currently accepted BMI formula, designed for more pragmatic purpose than scientific.