Experimental data of effect of mass on climbing speed
Someone pointed this blog post out to me.
 Climb by Bike
Climb by Bike
Interesting experiment: the rider (Luke, who went on to finish 26th in the Tour of L'Avenir) did L'Alpe d'Huez four times, each at close to 275 watts average power (measured with Powertap), trying different "treatments". In sequence, in the same day:
 Luke Rowe, who did four L'Alpe d'Huez repeats in one day in the name of science
Luke Rowe, who did four L'Alpe d'Huez repeats in one day in the name of science
So in these trials they got the following results:
Okay, so at first glance it appears the stuff designed to slow him down actually slowed him down. But then consider that the powers for each of the trials differ. Sure, they're fairly close, but then the times are fairly close, as well. So it's important to compensate for the differences in power.
First I'll use Tim Clark's Power-Speed converter to estimate the rider's weight. It comes conveniently programmed with the stats for L'Alpe d'Huez... So using the baseline run, assuming a baseline CRR = 0.4% and CDA = 0.36 m² with a drivetrain loss of 3%, and zero wind I get a rider + bike + equipment mass of 154 lb. Luke's a light guy, consistent with his photos.
So first I need to adjust for the difference in power among the different trials. I could do trial and error with Tim's script, but instead I'll use an analytic solution I blogged here. That result is a 1% change in power has an effect on speed of approximately 1% / (1 + 2 f), where f is the original fraction of power going into wind resistance. Using Tim's default parameters, I get approximately 6% of the power from these trials went into wind resistance, meaning a 1% change in power results in a 0.89% change in speed. With this conversion I get the following results for converting the power of each trial to 278 W:
normal bike: 49:40
3 bar: @ 9 sec (+0.3%)
water on bike: @ 1:44 (+3.5%)
water in wheels: @ 1:51 (+3.7%)
Again using the calculator I added 4 lb to the total weight (around 1.8 kg, adding only 14 g to the weight of water for the container and tape). The result was 1:04 added to the time. This differs considerably from the measured difference of 1:44. To match that difference, I need to boost the weight difference to 6.5 lb. So what's up with that?
One option might be that the container and tape is heavier than I give it credit for. Yet it seems unlikely that accounts for the full difference. Another possibility is that the rider lost weight between the second and third trials. Unless he was hydrating at 100% replacement level and did each ride with the same amount of water in his bottle, weight difference could easily account for at least half of this unaccounted weight difference. Another option is a difference in wind: even an imperceptible 1 mph headwind is worth 37 seconds. But an additional option is that the sloshing water is dissipating heat which comes in the end from the rider's power applied to the cranks. My money's on the principle factors being rider weight loss and a slight change in wind speed.
The most curious thing about these results to me is the small effect of a reduction in rolling resistance from approximately 8 bar (assumed) to 3 bar. Jobst Brandt's measurements showed a considerable increase of rolling resistance with this pressure reduction (the pressure axis uses units within 2% of bar):
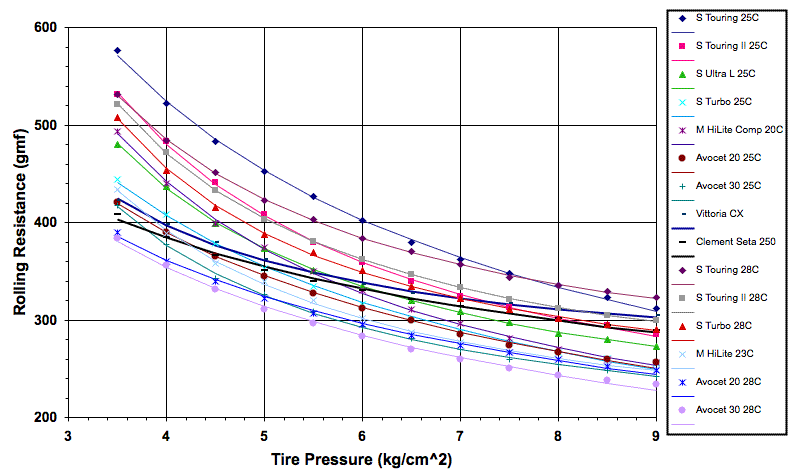
Rolling resistance accounts for around 28 seconds per 0.1% change from the assumed value of 0.4%. Rolling resistance is a big deal, and we're not seeing much of an effect here from either low pressure, or for that matter from the water in the tires.
So overall an interesting experiment. The conclusion? Weight really does matter on climbs (as the equations predict) but tire pressure may be over-rated. I should do my own field test: after all, all that's needed is a power meter, a timer, and a scale.
 Climb by Bike
Climb by BikeInteresting experiment: the rider (Luke, who went on to finish 26th in the Tour of L'Avenir) did L'Alpe d'Huez four times, each at close to 275 watts average power (measured with Powertap), trying different "treatments". In sequence, in the same day:
- Normal bike + 1.8L extra water in tires: Yes, you read that correctly: water was put in the tires. The goal was to determine the difference between the effects of rotating mass and translational mass on climbing times. Now the theory is simple enough: rotating mass makes it harder to change speed. In other words, harder to speed up, harder to slow down. Typically during a climb you speed up and slow down a lot: a bit each pedal stroke, in fact. So the magnitude of these speed changes is fractionally less with more mass in the tires relative to on the frame. But one speed increase is not canceled by an offsetting speed increase: the net speed change from start to finish. Suppose the rider started at rest and finished the climb at 9 meters/second, riding at constant power. Then the approximate effect of 1.8 kg (the mass of 1.8 liters of water) at the rolling radius on climbing time is ½ M vf² / P, where vf is the final speed, M is the extra mass, and P is the power. Plugging in 270 watts, 1.8 kg, and 9 meters/second yields 0.28 seconds. This is less than the timing resolution, so we'd expect no effect. On the other hand, that water moving around in the tire is going to create friction, and friction generates heat, and heat requires power. This will be result in an effective increase in rolling resistance.
- Normal bike + 1.8L extra water on bike: Now the water was mounted on the seatpost. It's still going to slosh around, creating heat, requiring power, but it certainly seems this effect should be a small fraction of the energy going into moving water in a tire. But that's just speculation. If speculation was all we needed, we'd not need to conduct any experiments.
- Normal bike: Nothing to say about this.
- Normal bike, reduced tire pressure only 3 bars: Hardly subtle; 3 bars (44 psi) is much lower than normal tire pressure of 8 bars (116 psi). Indeed for climbing time trials I prefer 10 bars (145 psi). More pressure = less tire deformation = less heat generated = lower rolling resistance. That's bike physics 101. Rolling resistance tests on smooth rollers always show this result. But for riding on rough roads, it's less obvious. In this case if the pressure gets too high, the bike bounces, raising and lowering the mass of the rider. This can increase rolling resistance: imagine the case of riding on a solid metal tire. It would work great on a steel rail (which is why trains don't use rubber tires) but on the road, it would be inefficient (not to mention uncomfortable). Still, 3 bar is typical of cyclocross, not riding on well-maintained roadways like the road from Bourg d'Oisans to Alpe d'Huez.
 Luke Rowe, who did four L'Alpe d'Huez repeats in one day in the name of science
Luke Rowe, who did four L'Alpe d'Huez repeats in one day in the name of scienceSo in these trials they got the following results:
- 52:01, 275w
- 51:34, 277w
- 49:40, 278w
- 50:38, 273w
Okay, so at first glance it appears the stuff designed to slow him down actually slowed him down. But then consider that the powers for each of the trials differ. Sure, they're fairly close, but then the times are fairly close, as well. So it's important to compensate for the differences in power.
First I'll use Tim Clark's Power-Speed converter to estimate the rider's weight. It comes conveniently programmed with the stats for L'Alpe d'Huez... So using the baseline run, assuming a baseline CRR = 0.4% and CDA = 0.36 m² with a drivetrain loss of 3%, and zero wind I get a rider + bike + equipment mass of 154 lb. Luke's a light guy, consistent with his photos.
So first I need to adjust for the difference in power among the different trials. I could do trial and error with Tim's script, but instead I'll use an analytic solution I blogged here. That result is a 1% change in power has an effect on speed of approximately 1% / (1 + 2 f), where f is the original fraction of power going into wind resistance. Using Tim's default parameters, I get approximately 6% of the power from these trials went into wind resistance, meaning a 1% change in power results in a 0.89% change in speed. With this conversion I get the following results for converting the power of each trial to 278 W:
normal bike: 49:40
3 bar: @ 9 sec (+0.3%)
water on bike: @ 1:44 (+3.5%)
water in wheels: @ 1:51 (+3.7%)
Again using the calculator I added 4 lb to the total weight (around 1.8 kg, adding only 14 g to the weight of water for the container and tape). The result was 1:04 added to the time. This differs considerably from the measured difference of 1:44. To match that difference, I need to boost the weight difference to 6.5 lb. So what's up with that?
One option might be that the container and tape is heavier than I give it credit for. Yet it seems unlikely that accounts for the full difference. Another possibility is that the rider lost weight between the second and third trials. Unless he was hydrating at 100% replacement level and did each ride with the same amount of water in his bottle, weight difference could easily account for at least half of this unaccounted weight difference. Another option is a difference in wind: even an imperceptible 1 mph headwind is worth 37 seconds. But an additional option is that the sloshing water is dissipating heat which comes in the end from the rider's power applied to the cranks. My money's on the principle factors being rider weight loss and a slight change in wind speed.
The most curious thing about these results to me is the small effect of a reduction in rolling resistance from approximately 8 bar (assumed) to 3 bar. Jobst Brandt's measurements showed a considerable increase of rolling resistance with this pressure reduction (the pressure axis uses units within 2% of bar):

Rolling resistance accounts for around 28 seconds per 0.1% change from the assumed value of 0.4%. Rolling resistance is a big deal, and we're not seeing much of an effect here from either low pressure, or for that matter from the water in the tires.
So overall an interesting experiment. The conclusion? Weight really does matter on climbs (as the equations predict) but tire pressure may be over-rated. I should do my own field test: after all, all that's needed is a power meter, a timer, and a scale.

Comments
carbon fiber bicycle accessories