Low-Key Patterson Pass: small groups and the prisoner's dilemma
The prisoner's dilemma is a description of a problem where you have two suspects are captured, accused of committing a crime, and are isolated in separate cells. If either admits to the crime while the other does not, the prisoner admitting to the crime is set free, the other given the most severe punishment (10 years in prison). If they both confess, they are given a light, 2 year sentence. If neither confess, they are held in prison for one year, but eventually freed for lack of evidence.
So if you're one of the prisoners, what do you do?
If they could collaborate, then the best approach would be for neither to confess. They'd esch serve a year in prison, which isn't great, but overall they'd serve only two years. That's much better than the alternates.
But they're isolated, so they can't collaborate. For each prisoner, what the other prisoner does is beyond their control. If the other prisoner confesses, then he is better off confessing as well, getting a 2-year sentence. If he does not, he'll get the maximum of ten years. On the other hand, if the other prisoner does not confess, then confessing means walking free, while not confessing means a year in prison.
So the best result for the group is cooperation. But if individuals act in their own selfish interest, then there will be no cooperation, and the net result is worse.
This is what happened in the group 2 small groups start at Patterson Pass yesterday. Groups were ordered by speed, based on prior scores or, in the case of a few brand-new riders, by considering results in other races, if any. The groups were thus fairly well matched within the group, but were still competing against each other. It was a mixture, therefore, of competing against the riders within your group and cooperating with the riders within your group.
The best overall result for the group was that everyone contribute on the early, relatively flat portion of the course. And by "contribute" I mean spend time at the front at a level of effort which will cause some fatigue, causing some loss of speed on the steep portion, but just a little. The payback in following the draft of other riders within the group, each of them also riding at a fatiguing pace when at the front, would more than compensate the loss.
However, without any way to enforce global cooperation, for each rider a better scenario is that everyone else does fatiguing pulls at the front, while that individual rider sits in and rests. Every rider in the group would prefer this to occur, so for every rider within the group the incentive is to sit in and rest, or if at the front to take a brief, low-power, non-fatiguing pull.
In group 1, one rider, Nils, hammers most of the way himself. This was good for the group, since Nils is freakin' strong on the flats, but it hurt Nils' result.
In group 3, there was a strong tandem with Paul McKenzie and Paul Chuck (this is Low-Key, so we allow all sorts of bikes to ride together). Tandems are well known for being strong on the flats, and in this case the tandem led the way along the flattish section, everyone else within the group benefitting.
But in group 2, we had no tandem, and we didn't have Nils. It was going to be up to each rider to contribute, and not enough did. I took the first pull, from the start line, and one other. That would have been more than enough given the length of the opening section and the number of riders (10) in the group.
But too many riders weren't working. They were playing to the prisoner's dilemma. As a result, group 2, which should clearly have been faster than group 3, lost substantial time to that group here, and of course we lost even more time to group 1. Our scores suffered as a result.
This is shown in the following plot. The plot uses only male solo scores, for consistency. I have two curves: the blue curve is the rider's best score in the most recent year for which that rider has a score, with older scores depreciated 1%/year. This is what I used for group assignments. The other curve is the average score for riders in the group on Patterson Pass.
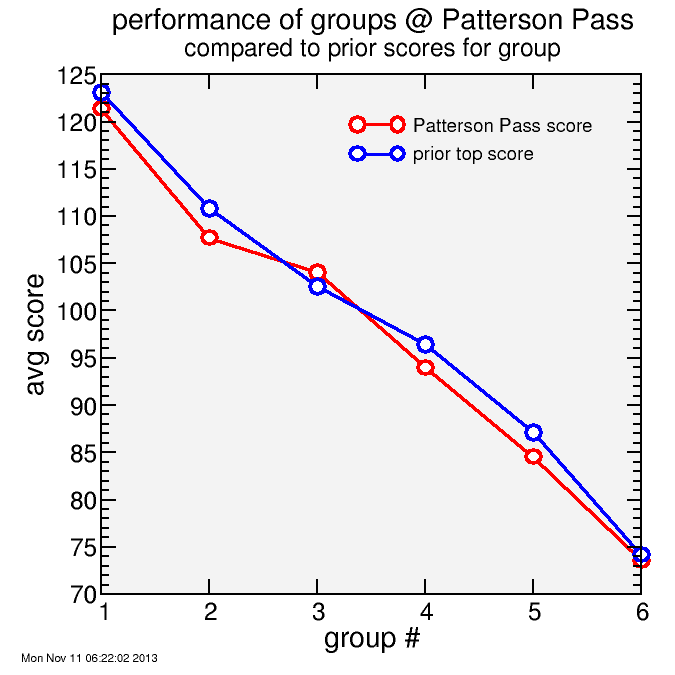
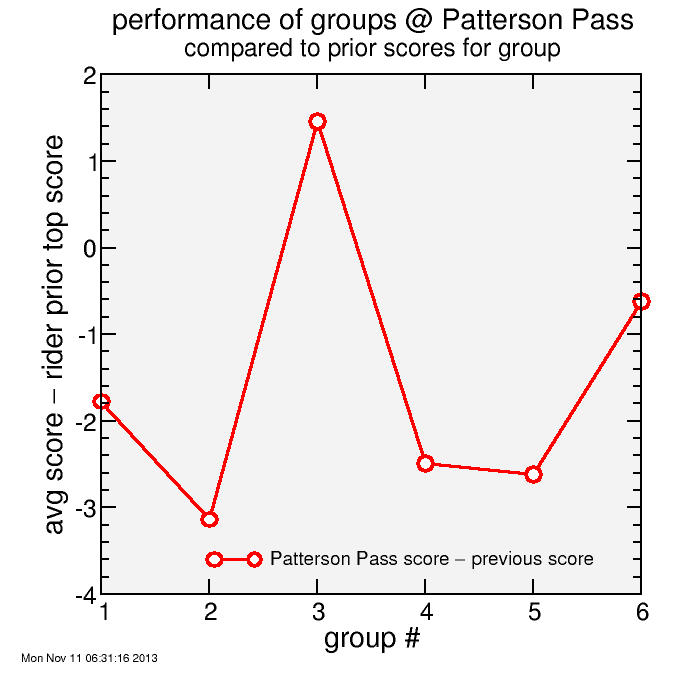
Although group 2 still did better than group 3, the differential between group 2 and their qualifying score is the greatest among all groups. It's clear group 2 could have done better overall, even if the "selfish" strategy may have helped some of the individual riders. Group 3, in particular, did well at Patterson due to the hard work of the tandem there. (Note: I fixed this from an initial version which showed group 6 also scored low. In the revision, where I restricted the comparison to riders for whom old scores existed. It's important the same riders contribute to both curves.)
Thanks to Paul McKenzie, here's the average speed of the groups on the first 1.3 miles:
From Paul:
My conclusion from this limited data is that Group 2 was indeed soft pedaling at the beginning, and conversely, Group 4 put in quite a cooperative effort, putting about 24 seconds on Group 2 during the first part of the climb. Those in our group (Group 3) received the benefit of a nice tow to the base leaving them with fresher legs for the climb.
This may seem unfair to members of group 2. But we dug our own graves. A great thing about bike racing is it's multiple facets. It's more than just a physical contest, it's also a mental game. And the prisoner's dilemma is a classic mental game.
By the way, this situation was very similar to handicap racing, where slower riders are given a head start, and the first across the finish line wins. There the penalty is more obvious, however: you can see your competitors up the road, or approaching from behind. Here the results aren't obvious until the math is complete on the start and finish times. But they're just as real.

Comments