Grade comparison: Devil Mountain Double versus Terrible Two

Back in January I proposed that road grades tended to follow cosine-squared probability distributions with the maximum grade as a parameter. Different roads could then be characterized by their maximum design grade. The choice of cosine-squared over the Gaussian which would be suggested by the Central Limit Theorem was because roads aren't random, they're designed, and designers impose a maximum grade beyond which the probability is exactly zero. This was important because I had proposed a heuristic speed formula for how long it takes a cyclist to ride a given road, and even for the rapid attenuation of probabilities associated with a Gaussian distribution, the cycling time would have been dominated by pathologically steep grades. Using cosine-squared this issue went away.

Anyway, I got curious as to how the Devil Mountain Double course compared with the Terrible Two course in that regard. Which is steeper, and do both tend to follow the superposition-of-cosine-squared probability distributions I proposed?

In each case, I did the fits "by eye". I made no attempt to match the total climbing in the actual profiles with the total climbing from the analytic fits, except for a crude check on Devil Mountain Double due to a fit that wasn't as good as for Terrible Two (more on that a bit later). I smoothed the profile with a bi-exponential smoothing function of characteristic length 50 meters, then partitioned the profiles into 50 meter segments, and did a histogram of the grades from these 50 meter segments. These thus don't represent the maximum peak grades on the courses, for example at particular switchbacks, but rather the grades which are sustained over at least 100 meters or so.

For Terrible Two, I had previously done a crude fit to the grade distribution. I redid the fit more carefully here:

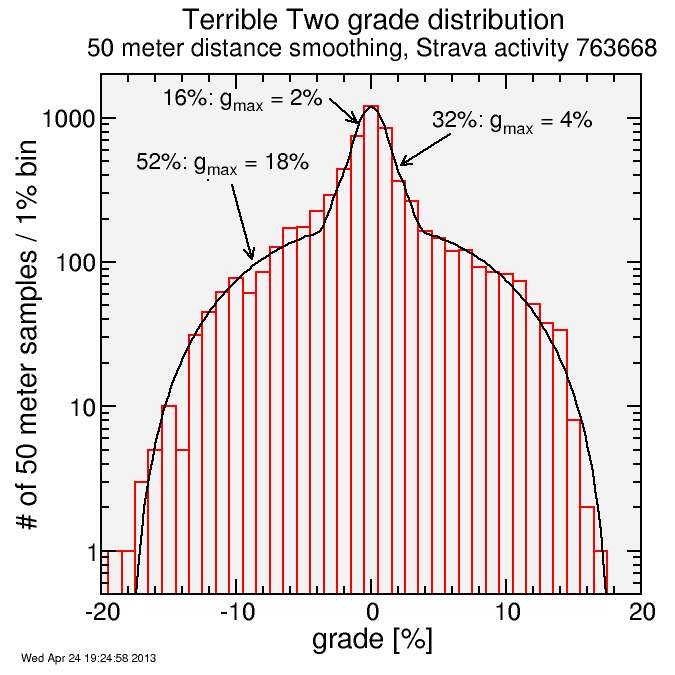
I modeled the grade for the Terrible Two course assuming a trimodal distribution: there's three types of roads:

1. 52% of the total distance is steep mountain roads, where the maximum grade is 18%.
2. 32% of the total distance is rolling roads where the maximum grade is 4%
3. 16% of the total distance is flat roads where the maximum grade is 2%.

The distribution is fairly symmetric, with the climbs similar to the descents.

In contrast, here's the result for the Devil Mountain Double course:

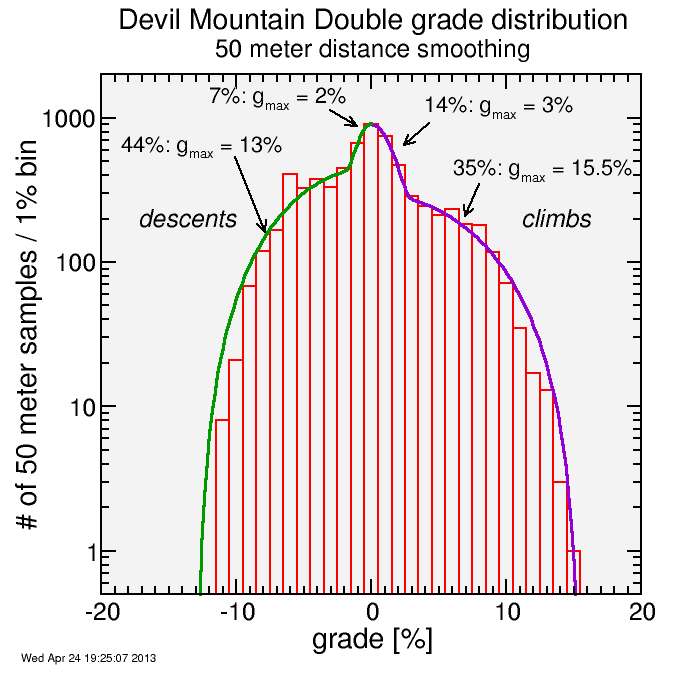
The first thing which you might notice relative to Terrible Two is the strong asymmetry here. The climbs are steeper, in general, then the descents. This is essentially due to the two climbs: Mount Hamilton and Sierra Road. For Mount Hamilton, the particular requirement that heavy hardware be hauled up to the summit for the creation of the Lawrence Livermore Observatory imposed an imperative on gradual grades on the western side (Mount Hamilton Road). The eastern side, free from such a requirement, was able to be built (as San Antonio Valley Road) taking a much more direct route up the hill. The other is Sierra Road. Sierra, the climb which follows the descent from Hamilton, is a steep climb which is followed by the more gradual Felter road descent. These two climb-descent pairs weight the distribution in favor of steeper climbs and more gradual descents.

I separated climbs and descents to yield the following:

1. 44% of the total distance is mountain descent, where the peak grade is 13%. Note the hump which rises from the shoulder of this distribution. That's Mount Hamilton Road, which has a particularly uniform grade for each of it's three primary descents. I did the fit as a compromise between the Mount Hamilton Road hump and the rest.
2. 7% of the total distance is essentially flat but descending, with a peak grade of 2%
3. 14% of the total distance is essentially slightly rolling but climbing, with a peak grade of 3%.
4. 35% is steep climbing, where the peak grade is 15.5%.

So with this approximation, 48% of Terrible Two is flat or rolling, while only 21% of Devil Mountain Double is. But the climbs and the descents of the mountainous portion of Terrible Two is steeper, with a maximum grade of around 18%, while the steep roads of Devil Mountain Double max out at "only" 15.5%, and the descents avoid major steepness with a max grade of 13%. The initial descent from Mount Diablo summit clearly peaks steeper, but it's so short that the rounding and interpolation scheme used to generate the plot reduces the peak a bit (the focus is on sustained grades, which are more significant).

The result? Devil Mountain Double ends up with more vertical feet, but the descents are faster (more gradual grade means less of the potential energy wasted in safety-motivated braking). And without the real leg-breaking climbs of Terrible Two, pacing on hills is easier to control. What isn't shown here is the wind generally blowing riders down the coast to Fort Ross in Terrible Two. This, combines with less total climbing, makes Terrible Two net faster.