boat puzzle: still confused
Back to the boat puzzle...
I freely admit this is perhaps among the most boring topics ever posted to a blog in this history of the Intenet. But I feel the irrational need to put some sort of closure on this.
I proposed that all solutions to the arbitrary boat puzzle could be reduced to the simple example of Mac-Nadia-Flannel.
It was first proposed to me that if there is at least one member not a part of a maximal independent set incompatible with no more than two members of the maximal independent set, the problem can always be solved. This is true: just leave everyone else on the boat and solve the simple Mac-Nadia-Flannel-cans problem with the one remaining seat.
But there's a more general approach, in which each elemnt of the "Mac-Nadia-Flannel-cans" puzzle is represented by a group rather than an individual. First, identify which animals which are going to go across on the first trip (the rest are a maximal independent set). Then bring the rest across. Then decide which of those from the first trip will stay on the second shore, and which will stay on the boat for the duration of the entire solution. Next, make trips to shuttle across those in the independent set compatible with those left on the second shore. Then shuttle across a first group not compatible with those on the second shore. Swap these animals with those left on the second shore, bringing those back. Then swap these for the last of the animals left on the first shore. Finally, head back, pick up everyone else, and shuttle them across.
For this to work, the number of animals originally left on shore 1 who are incompatible with those originally left on shore 2 must number no more than twice as many as those originally left on shore 2.
Anyway, that's a lot of detail. I wrote a program to carry out this solution. I first generated either all possible puzzles (for up to 8 animals) or a set of 8192 random puzzles (for up to 16 animals here ... 3, 9, and 13-16 had no failures). The fraction of puzzles which could not be solved is as follows. You see this captures most cases.
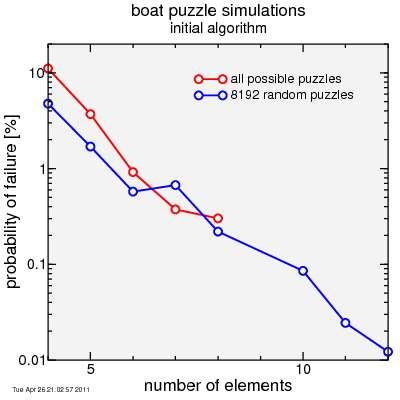
So you can see the algorithm does pretty well.
However, I felt the solution was too general. It was making too restrictive assumptions about the individual groups. So I checked my code for simple rejected cases and identified the following as a solvable puzzle. The unique maximal independent set is outlined:
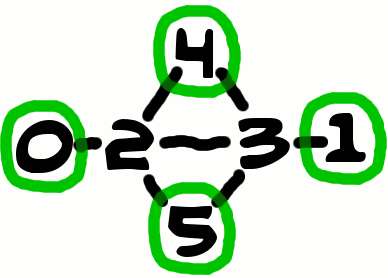
This problem can be solved.
In considering the solution of this problem, we observed that after swapping 1 and 2, swapping 2 and 3, and swapping 4 and 5 the reverse solution ("playing the video backwards") is the same as the forward solution. That's curious. There's an underlying symmetry here which is being exploited. Indeed, I think it can be shown that the optical solution of any puzzle is also an optimal solution when played backwards. In the case of a symmetric puzzle an optimal solution exists where the puzzle played in reverse is the same as the forward solution after swapping symmetric pairs.
But I was never very good at abstract math...
I freely admit this is perhaps among the most boring topics ever posted to a blog in this history of the Intenet. But I feel the irrational need to put some sort of closure on this.
I proposed that all solutions to the arbitrary boat puzzle could be reduced to the simple example of Mac-Nadia-Flannel.
It was first proposed to me that if there is at least one member not a part of a maximal independent set incompatible with no more than two members of the maximal independent set, the problem can always be solved. This is true: just leave everyone else on the boat and solve the simple Mac-Nadia-Flannel-cans problem with the one remaining seat.
But there's a more general approach, in which each elemnt of the "Mac-Nadia-Flannel-cans" puzzle is represented by a group rather than an individual. First, identify which animals which are going to go across on the first trip (the rest are a maximal independent set). Then bring the rest across. Then decide which of those from the first trip will stay on the second shore, and which will stay on the boat for the duration of the entire solution. Next, make trips to shuttle across those in the independent set compatible with those left on the second shore. Then shuttle across a first group not compatible with those on the second shore. Swap these animals with those left on the second shore, bringing those back. Then swap these for the last of the animals left on the first shore. Finally, head back, pick up everyone else, and shuttle them across.
For this to work, the number of animals originally left on shore 1 who are incompatible with those originally left on shore 2 must number no more than twice as many as those originally left on shore 2.
Anyway, that's a lot of detail. I wrote a program to carry out this solution. I first generated either all possible puzzles (for up to 8 animals) or a set of 8192 random puzzles (for up to 16 animals here ... 3, 9, and 13-16 had no failures). The fraction of puzzles which could not be solved is as follows. You see this captures most cases.

So you can see the algorithm does pretty well.
However, I felt the solution was too general. It was making too restrictive assumptions about the individual groups. So I checked my code for simple rejected cases and identified the following as a solvable puzzle. The unique maximal independent set is outlined:

This problem can be solved.
In considering the solution of this problem, we observed that after swapping 1 and 2, swapping 2 and 3, and swapping 4 and 5 the reverse solution ("playing the video backwards") is the same as the forward solution. That's curious. There's an underlying symmetry here which is being exploited. Indeed, I think it can be shown that the optical solution of any puzzle is also an optimal solution when played backwards. In the case of a symmetric puzzle an optimal solution exists where the puzzle played in reverse is the same as the forward solution after swapping symmetric pairs.
But I was never very good at abstract math...

Comments