boat puzzle:: the first trip and maximal independent sets
I'll now continue my discussion of the boat puzzle in which the goal is to get cats across a river in a boat, where there are fewer seats on the boat than cats, and certain cats must not be left with each other unsupervised.
For the first trip across the goal is simple: to leave no two incompatible cats back on the first short. For example, consider the following problem, with cats Mac, Nadia, and Flannel, where I spiced it up slightly with the requirement to also transport a supply of cat food cans:
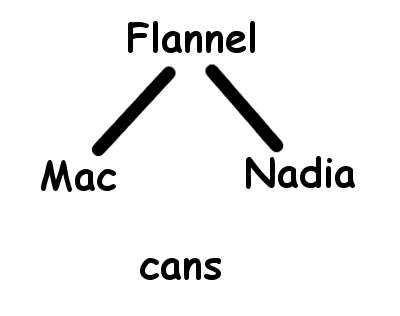
I want to find a group which has no mutual connections to leave back on the shore. Ideally, my boat should require no more seats than the number of cats + objects to be transported in that first trip. Thus I want this group without mutual connections to be as large as possible. The largest group without connections is called the maximal independent set.
Here is the maximal independent set for the graph shown above:

The only element not in the maximal independent set is Flannel, so Flannel goes in the boat first, and I need at least one seat in the boat to accomplish my task (which is obviously the minimum for any non-zero number of cats + objects).
If I have two seats, there is a trivial (perhaps nonoptimal) solution. I keep Flannel in one seat, while I use the other seat to transport cats across one-by-one. For example, I take Flannel + Mac, drop off Mac, go back with Flannel, pick up Nadia, drop Nadia off with Mac (leaving Flannel on the boat), go back with Flannel, pick up the cans, then exit the boat with Flannel and the cans: all across. The interesting question is if I can solve it with only enough seats to isolate the maximal independent set.
Here is another graph I described last time: Flannel, Mac, and Molly: none of the two cats can be left together unsupervised.
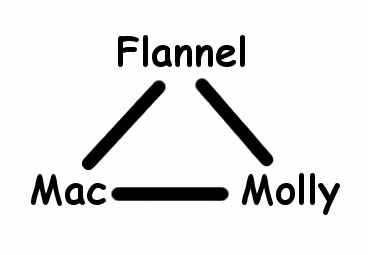
Here there are three candidates for the maximal independent set, each with only one member:
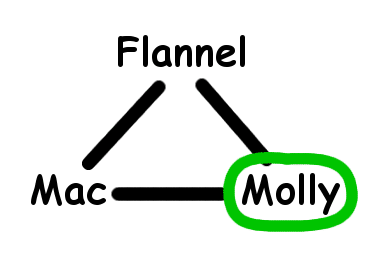
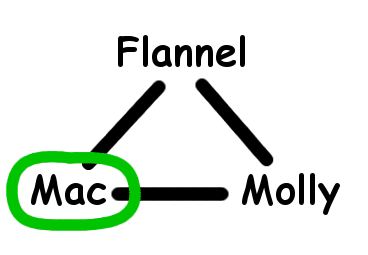

So I need at least two seats to solve this problem. And I can solve it with two seats: for example, I pick Molly as my independent set, and put Mac and Flannel in the boat. I drop off Flannel, and take Mac back. Then I pick up Molly and take Mac and Molly and I'm done.
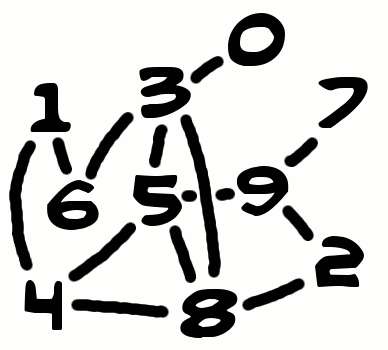
The whole trick is in finding a maximal independent set which allows the problem to be solved with just enough seats on the boat to carry the others across on that first trip. Here is a randomly generated graph. The Perl code which generated this plot isn't very creative, so used numbers for the elements of the graph, as opposed to cat names:
There are three solutions for the maximal independent set here; here is an arbitrary one:
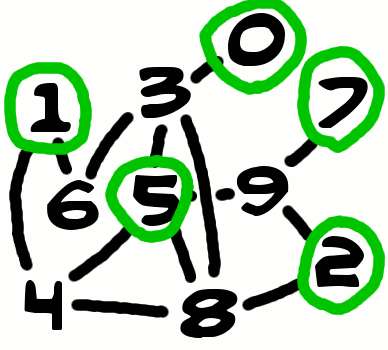
You can see I would need five seats on the boat to make the first trip. So the question is: is this enough? As I described, there is a trivial solution if there are six seats on the boat, so I want to solve it with only five.
For the first trip across the goal is simple: to leave no two incompatible cats back on the first short. For example, consider the following problem, with cats Mac, Nadia, and Flannel, where I spiced it up slightly with the requirement to also transport a supply of cat food cans:

I want to find a group which has no mutual connections to leave back on the shore. Ideally, my boat should require no more seats than the number of cats + objects to be transported in that first trip. Thus I want this group without mutual connections to be as large as possible. The largest group without connections is called the maximal independent set.
Here is the maximal independent set for the graph shown above:

The only element not in the maximal independent set is Flannel, so Flannel goes in the boat first, and I need at least one seat in the boat to accomplish my task (which is obviously the minimum for any non-zero number of cats + objects).
If I have two seats, there is a trivial (perhaps nonoptimal) solution. I keep Flannel in one seat, while I use the other seat to transport cats across one-by-one. For example, I take Flannel + Mac, drop off Mac, go back with Flannel, pick up Nadia, drop Nadia off with Mac (leaving Flannel on the boat), go back with Flannel, pick up the cans, then exit the boat with Flannel and the cans: all across. The interesting question is if I can solve it with only enough seats to isolate the maximal independent set.
Here is another graph I described last time: Flannel, Mac, and Molly: none of the two cats can be left together unsupervised.

Here there are three candidates for the maximal independent set, each with only one member:



So I need at least two seats to solve this problem. And I can solve it with two seats: for example, I pick Molly as my independent set, and put Mac and Flannel in the boat. I drop off Flannel, and take Mac back. Then I pick up Molly and take Mac and Molly and I'm done.
The whole trick is in finding a maximal independent set which allows the problem to be solved with just enough seats on the boat to carry the others across on that first trip. Here is a randomly generated graph. The Perl code which generated this plot isn't very creative, so used numbers for the elements of the graph, as opposed to cat names:

There are three solutions for the maximal independent set here; here is an arbitrary one:

You can see I would need five seats on the boat to make the first trip. So the question is: is this enough? As I described, there is a trivial solution if there are six seats on the boat, so I want to solve it with only five.

Comments