boat puzzle: solving the simple cases

Previously I described the boat puzzle and how it's provided some mental exercise for my train commutes.

The traditional example is the Mac-Flannel-Nadia case:



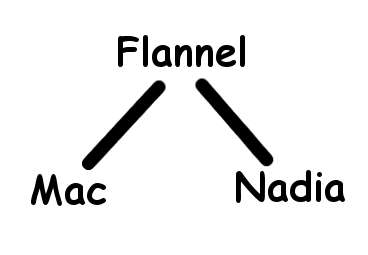
The solution, as I described, is to identify a maximum independent set, in this case Mac and Nadia. Then you need a number of seats on the boats sufficient to transport the rest, in this case Flannel. So:

1. Flannel taken from shore A to shore B.
2. return with empty boat.

Next step doesn't matter, as Mac and Nadia are identical in this problem. I'll pick Mac:
3. Mac taken from shore A to shore B.

Now Mac and Flannel are together. I need to return with Flannel on the boat, as I cannot leave the two, or Mac will turd.

4. Flannel taken from shore B to shore A (leave Mac on B).

But then....

5. Take Nadia from A to B (leave Flannel alone). Nadia is now with Mac, and they lick each others faces, so that's fine.
6. Return with empty boat.
7. Bring Flannel from A to B.

When I add in the cans, it's only slightly more complex. I circle the maximum independent set, the cats which need to be left behind on the first boat trip:

Mac-Nadia-Flannel-cans

Here I add steps between steps 2 and 3 in the above:

2.1 bring cans from shore A to shore B. Leave those with Flannel, who can't open them.
2.2 return with empty boat.

Then continue with step 3.

Here is a problem which cannot be solved in a nontrivial number of seats on the boat. Recall if I have more than the number of seats sufficient to isolate the maximum independent set, then a solution becomes trivial, so I am only interested in problems with non-trivial solutions.

Another problem: I add Joshua to Mac, Nadia, and Flannel. Joshua is very friendly, but Flannel is a pest, and due to certain issues, Joshua can't defend himself as well as he might. So I don't want to leave Joshua with Flannel, either. The maximal independent set is obviously Joshua, Nadia, and Mac. I therefore want to be able to solve it with only one seat on the boat:

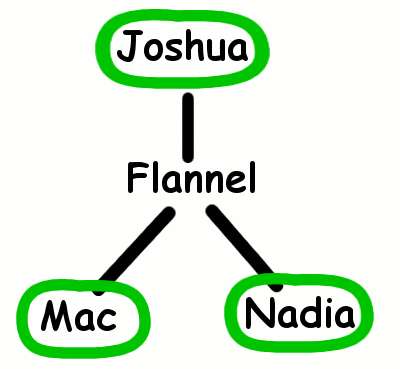
Mac-Nadia-Flannel-Joshua


Out of luck here: I know of no solution.

So I conjectured that all problems can be reduced to either Mac-Nadia-Flannel-cans or Mac-Nadia-Flannel-Joshua. If the former, I can solve them. If the latter, I cannot. That was my conjecture, but I no longer believe it to be true.

Comments

Post a Comment

Popular posts from this blog

Marin Avenue (Berkeley)

Image
On Saturday, I got an email from Tim telling letting me know that Murphy's Spring Classics was going to start up Marin Ave. I'd missed that. Murphy announces his courses the day before, and indeed it was already well into the night before when the course announcement went out. I'd skipped over the details, jumping straight to middle and end games. Marin? I laughed at the irony, because not long before when he'd told me he was choosing to repeat the Nifty Twn Fifty which we'd done together last year versus selecting Murphy Mack's Stage Mullett two-day, I responded I didn't think I had it in me to ride Marin Ave two years in succession. Well, so much for that. I was committed, so I went downstairs to swap my 11-26 cassette for my Recon 12-27. The name is easily overlooked: "Marin Ave" fails to strike the same impression as, for example, "Redwood Gulch" or "China Grade". But among those in the know, Marin Ave is infamous i...
Read more

hummingbird feeder physics

Image
I couldn't figure out how the hummingbird feeder worked. Why didn't it overflow? Forces need to balance, of course. Neglecting surface tension, there liquid level is higher in the inner reservoir than in the feeding chamber, so there must be a corresponding pressure difference. Suppose the pressure in the inner chamber were zero. Then the column height difference would need to be atmospheric pressure / (density of liquid × gravity). But this is over 9 meters! Obviously the height difference is only approximately 1% of this. So the pressure difference inside versus outside is only approximately 1%. The inside is only slightly below atmosphere. So air is getting in. How? Does it diffuse through the liquid? If this were the dominant mechanism, it wouldn't take long for the pressure inside to go from 99% to 99.3%, for example, which should be plenty to push the column of liquid down in the inside chamber and thus push liquid out through the holes. It would over...
Read more

Gallium Pro geometry

Image
On Caltrain yesterday, I was surprised to see among the usual set of commuting bikes a SRAM Red-equipped Argon Gallium Pro. The bike immediately stole your attention. The design was one which has been trending: clear-coated carbon with plenty of text detail so the viewer is sure to realize he's gazing upon the result of advanced, proprietary engineering and not at yet another paint job on the same old OEM frames being pumped out of the same old Taiwanese factories. But it worked: the bottom bracket area was huge, the downtube a large-diameter "inverted Kamm tail" design seemingly designed to maximize wind resistance, the top tube a broad, eccentric shape which screamed "vertically compliant yet torsionally stiff". All it lacked were the pencil-think seat stays Cervelo popularized, but this was a machine designed for stiffness over anything else. It seemed dramatic overkill, since the bike was small (the Argon "XS" I suspect). There wasn't muc...
Read more