On Stages cadence, and comparison w/ Powertap from DC Rainmaker data
In the previous post I compared power from the Stages power meter to power from the Vector power meter (or meters, since L and R are separate) measured by DC Rainmaker on a ride he did in DC after the Vector release in Boulder, Colorado. Since Stages is measuring power only on one side of the bike, it is natural to compare the results with Vector, which measures power on each side of the bike separately. Before that, I showed that the Vector total power agreed well with Powertap and Quarq. If I assume that validates total power for the Vector, then it validates L and R power separately, since total power is derived from L and R power (the validation would be invalid if there were errors which naturally canceled between the L and R side, but I can't identify any).
But Stages does one thing I really like: it measures cadence multiple times per second, instead of relying on an average cadence associated with the time for a full pedal rotation. The constant cadence approximation leads to an error if the pedal velocity is changing during the pedal stroke, as it would if the bike is in a low-inertial condition such as a steep climb or strong headwind or resistive surface like mud or sand, or if the bike had eccentric chainrings. I wrote about this in 2010. Quarq makes the constant cadence approximation, since it uses a magnet to measure pedal rotation time.
Vector, on the other hand, may or may not make this approximation. I don't think they've said how they measure cadence. It's not trivially obvious, since there's advantages and disadvantages. The disadvantage I've described. The advantage is that it's relatively easy on a trainer, where the crank is spinning isolated in inertial space, but when riding on rough roads at low cadence it's not easy to measure instantanous cadence accurately. I described this in 2010, as well.
Stages would need to measure cadence differently than the way I described Vector might do it, since they operate on only one side. What Stages does, I suspect, is to put accelerometers at two separate radii of the crank arm, two different positions in their package. The difference in acceleration between these points is easily calculated: 𝞈² Δr, where 𝞈 is the angular velocity of the crank (radians/sec) and Δr is the separation of the accelerometers. So if I can measure that acceleration difference, I can extract the rotation rate: 𝞈 = sqrt[Δa / Δr], where Δa is the acceleration difference.
The nice thing about this is it doesn't depend on the position of the Stages along the crank arm, it just depends on the accelerometer separation, and that's essentially fixed by the rigid package. The challenge with this, especially when 𝞈 is relatively small, is that for Stages, Δr is just a fraction of the crank arm length, so the magnitude of this acceleration difference is limited. They would do better if they had a greater package length.
We know vibrations are on order 1 g, where g is the acceleration of gravity. So it's useful to compare the expected acceleration to this reference. If the cadence = 40 rpm (2/3sec) and the accelerometer separation is 2 cm, the acceleration difference would be 36 milligravities. So to estimate that to within 1% accuracy (you likely need at least this good for 2% power accuracy) would require 360 microgravity sensitivity in the presence of noise on order gravity. So it's nontrivial as your bike is rattling over the cobbles.
So the question becomes: how well can they cancel other sources of vibration this way? Vibrational modes of the crank arm, for example, will result in differences in acceleration at different point along the crank arm and will yield an error in cadence extraction.
Anyway, if they can get the cadence sufficiently rapidly, for example 3 times per half-pedal-stroke, which at 180 rpm is 18 times per second, they should do a superior job than other power meters at reproducing what Powertap measures, which is power without relying on imprecise approximations for cadence as a function of time. So I compared Stages "total power" to Powertap power. Here's a histogram of the power difference:
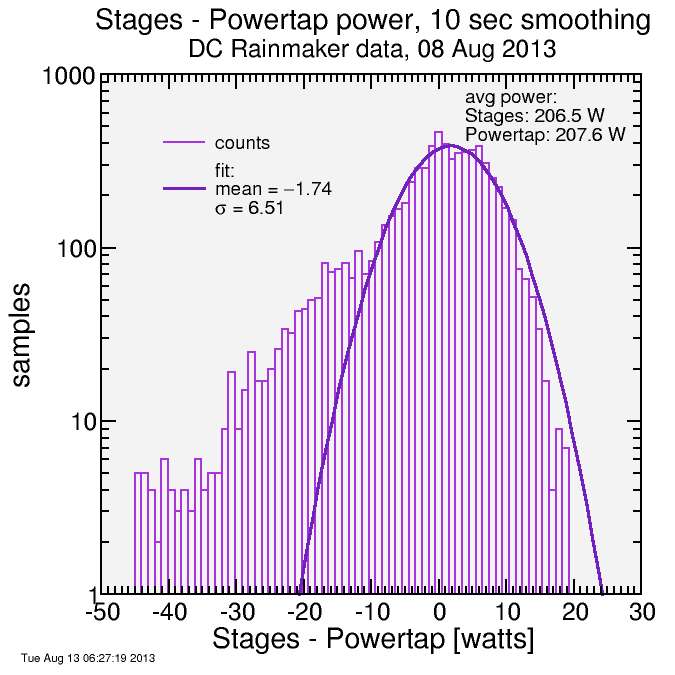
First, don't panic: it's not as bad as it looks. First of all the axis is logarithmic, which enhances small counts. Second, recall power differences can come from timing differences as well as actual differences in power measurement, and no two power meters (and head units) are going to be perfectly synchronized. That said, there's still a lot of spread there compared to the other comparisons I've done. Recall Quarq and Vector both tracked Powertap rather nicely. If all you looked at was average power, you'd be extremely pleased with this comparison, however (unless you factored in drivetrain loss of on order 7 watts, in which case you'd be slightly less happy). In any case I've never heard anyone complain about Stages accuracy or precision. The reality is most people aren't very sensitive to either.

Comments
I miss the old Metrigear days of total transparency :).