pVAM and the Critical Power Model
This Tour de France has experienced truly epic increases in people calculating how much power riders generate on climbs, typically towards assessing whether Chris Froome is practicing illicit performance enhancement. One of the more popular practioners of this assessment is VeloClinic, for example in his Haiku-esque Tumblr page.
In previous years, there has been a good deal of discussion about VAM, Ferrari's statistic of rate of vertical ascent. Since climbing primarily involves mass overcoming gravity, VAM is related to power/mass, but but it's only a crude instrument, since the more gradual the climb, the greater the fraction of power going into wind resistance and rolling resistance. Additionally, it is possible to sustain higher VAM for shorter climbs compared to longer ones: on shorter climbs you can use your anaerobic energy reserves more rapidly, increasing the energy per unit time, which is power. Furthermore, at higher altitude oxygen concentrations in the atmosphere are less, so it becomes more difficult to produce a given threshold of power. For all of these reasons, comparing against a fixed VAM is misleading. On steep, short climbs at low altitude you get a big number and all of a sudden you become suspicious the rider is doping, while for an extended, less steep climb like Ventoux (climbed today in the Tour) you get a lower number and conclude everything is good.
To address this, VeloClinic describes a new variable, pVAM, which represents the VAM a top Grand Tour rider would have been able to attain on a given climb during the biological passport era, 2009-2013. The formula is:
pVAM = 2885.17 + 416.825 ln Gradient - 0.06197 VClimb - 0.08796 Altitude
There's a bunch of issues with this, for example it fails to consider where the climb falls within the race or within a stage. A short stage ending with a climb early in a stage race is going to produce a higher VAM than a climb which is part of an epic stage late in the stage race. Still, it's a step in the right direction, and nice work, as long as the limitations are recognized.
But my greater concern is the use of a linear fit. It's generally considered that power is the limiting factor on climbs, that on shallow climbs and steep climbs, riders can ride to a certain power, and the VAM differences are due to differences in the fraction of total power which goes into overcoming gravity. There's a standard model for this, which I have used often in this blog (it's being called the "CPL model" on Twitter, after the Cycling Power Lab website which allows you to calculate it).
Additionally, for the length of the climb, the more time it takes to climb a hill, the lower the power a rider can produce. This effect is treated in the pVAM formula with a linear dependence. But there's a simple model for this which has been vetted in the peer review literature, and that's the critical power model (CPL website page).
So rather than rely on a linear model, an alternate approach is to assume constant power, that power a function of climb duration using the critical power model. For that, I need parameters. So I'll assume a critical power of 6 W/kg (Powertap: equivalent to a slightly, for example 3%, higher power at the crank), and an anaerobic work capacity of 90 seconds times the critical power, which is 540 J/kg. These numbers might be exemplary of an exceptional Tour de France climber.
Note this becomes an implicit calculation: to calculate VAM I need power. To calculate power I need the duration of the climb. To calculate the duration of the climb I need VAM. So I need to iterate until the solution converges. That's handled easily enough with Perl scripts I wrote long ago.
Then there's the altitude effect. I neglect that in my calculations, but there's plenty of on-line references for how sustained power varies with altitude (for example, in the CPL site). I could easily add these to my scripts. It would reduce my VAMs somewhat but the shape of the curves would be very similar.
I compare two situations: one is a 7.3% grade climb of different net climbing. 7.3% is the mean grade of Old La Honda Road, and I consider it the canonical climbing grade. The next one is to fix the climbing at 1000 vertical meters and vary the grade. 1000 meters is typical of a hard climb in the Pyrennees or Alps.
First, the total climbing plot:
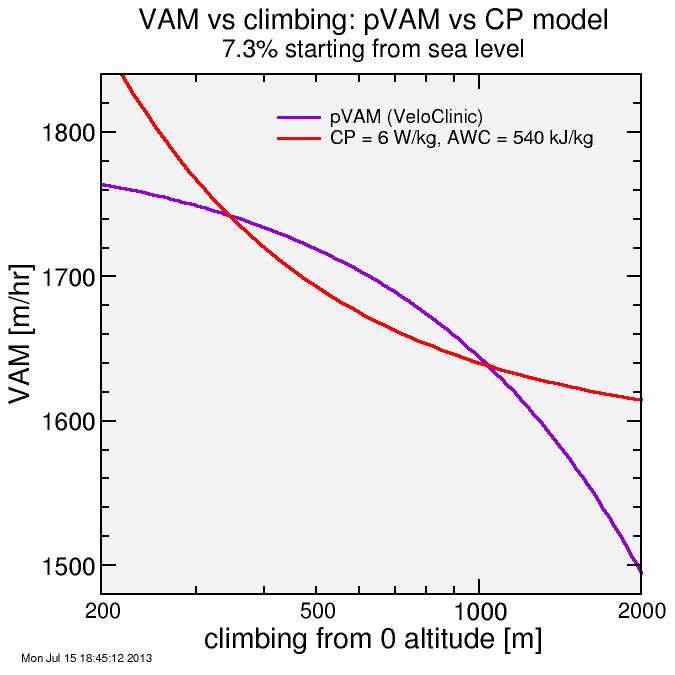
The parameters I chose for the CP model are rather arbitrary, so I don't expect the two curves to line up, but I would expect the shape to be similar. But they don't: the pVAM curve has a substantially different shape than the one calculated using the CP model. The CP model is simplistic, for sure, so I don't claim it's a gold standard, but at least it's been validated against a range of experiments, so I trust it more than an arbitrary linear model.

Here again, under the assumption of grade varying, the linear model used in the pVAM calculation deviates substantially from the use of the bike speed-power equations and the CP model.
So what sort of differences does this represent? On short climbs and long climbs, the CP model predicts higher VAMS than pVAM. And on both gradual and steep climbs, the CP model predicts lower VAMs than the pVAM model.
The result is that one needs to be careful when using the pVAM model for climbs which deviate substantially from the "average" climb used in the fitting, assuming the assumptions used here are applicable: 1. that the CP model predicts how the power varies with duration of effort, and 2. that riders tend to produce the same power for different grades for a given duration of effort.
Since I tend to trust power calculations more than linear fits, what I would be looking at is the predicted critical power for riders based on efforts they can generate on a given climb. To get this, you need a number for anaerobic work capacity. Set this to some time multiplied by CP, for example 90 seconds, or treat it as a fitting parameter in analyzing historical data. By looking at CP (critical power) the duration of the climb is eliminated. Then if you want to add an altitude effect, make it CP at sea level (or some other reference altitude).

Comments
I'm wondering if Strava uses a formula or crowdsources its Watt estimates. In either case, they'd have massive data sets to model pVAM. I suppose that could be another metric they provide, pVAM, the purpose of which would be to determine riders' acclimation to altitude.