yaw angle: variable wind speed and variable rider heading

Here's my fourth post in my series where I try to derive a probability distribution for yaw angle. I ask myself why I spent so much time on it, but it became something of a silly obsession, and I suppose as far as temporary obsessions go it isn't so bad. I could have been doing Sudoko or doing crosswords, for example, or playing games on my new "smart" phone. Or worse, responding to work emails and studying manuals or reading literature.

Anyway, here's the equation I derived:

P(yaw) ∝ 2 cos yaw / sqrt [ γ² ‒ sin² yaw ]

First I want to integrate this to derive an analytic normalization constant. For that I cheated and used the Wolfram Integrator:

2 arctan [ sin yaw / sqrt ( γ² ‒ sin² yaw ) ]

which integrated across allowed values of yaw yields 2 π. In retrospect this is obvious, as this is the range of headings I'm considering, and I'm normalizing over all headings. So I can write the normalized result:

P(yaw) = cos yaw / (π sqrt [ γ² ‒ sin² yaw ])

One interesting case is where γ → 1. Then:
P(yaw) ≈ cos yaw / (π sqrt [1 ‒ sin² yaw ])
= 1 / π.

This says all values of yaw with positive cosine are equally likely in this case.

Here's that plot of the result again.



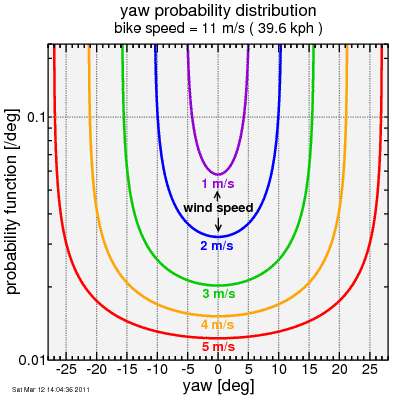
You can see the probability is U-shaped, with a peak at the maximum yaw angle. This is important, because when Hed says there is a peak in the yaw distribution, that peak in this case is not the average yaw, but the maximum.

The maximum yaw angle can be calculated by setting the denominator to zero:

sin yaw = ±γ

The maximum yaw goes from 0 for 0 wind up to 90 degrees for wind equal to the bike speed. Note this is not what you get if you assume the wind is coming directly from the side: that would be tan yaw = ±γ. For small values of γ the two are approximately the same, and thus for very light wind the maximum yaw happens in a direct cross-wind, but the maximum yaw when the wind is nearly as fast as the rider actually occurs when the wind is almost directly behind the rider.

The next step is to combine the distribution of yaw angles at a given wind speed with the distribution of wind speeds. So I want to integrate over all possible wind speeds the probability of that wind speed multiplied by the probability for yaw at the given wind speed. This gives me a net probability for the given yaw in the presences of changing wind.

Now recall the wind speed probability is peaked, just like the yaw probability at a given wind speed:



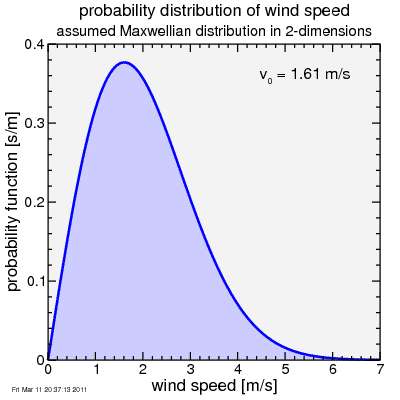
So if you consider the cross-wind case for example, and assume the rider is moving at a given speed, then the yaw angle would also have a non-zero value at its maximum probability. But the rider isn't riding at a constant heading relative to the wind.

Note for a given yaw angle there is a minimum wind speed (or γ) which will provide that yaw (lower γ values do not contribute);

γ_min = sin yaw

So what i want is;

P(yaw) = ∫ [sin yaw to ∞] dγ ( γ / γ₀² ) exp[‒ γ² / ( 2 γ₀² ) ] cos yaw / (π sqrt [ γ² ‒ sin² yaw ])

with:

γ₀ ≡ v₀ / s.

Amazingly, I was able to evaluate this analytically, again with the help of The Integrator:

P(yaw) = cos(yaw) × exp[-sin²(yaw) / 2 γ₀²] / (sqrt(2π) γ₀)

Now, when I look at that I am forced to think the process I took to evaluate it was far, far from optimal. But all that matters is the final answer, right? In any case, since I need to put this behind me, I'm not going to return to try and find where I went astray.

Here's a plot:



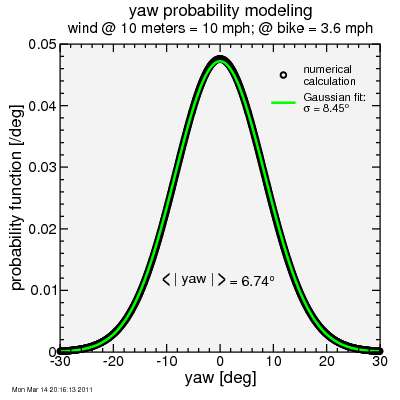
I show both the calculated net yaw probability and a Gaussian I fit to the same data.

Curious: i started with two probability distributions, each with a peak at non-zero, and I end up with a net probability distribution with a peak at zero. But this is basically what the central limit theory says; if you combine probability distributions, the result tends to become more Gaussian. A Gaussian probability distribution is called the "normal" distribution, after all.

So the end result of all of this is that, given the assumption of an average 10 mph wind at 10 meter elevation (a stiff wind), a Maxwellan distribution of the ratio of wind speed to rider speed, an average rider speed of 11 m/sec (40 kph), and a Hellman coefficient of 0.34 (associated with urbanized areas), I get the average yaw angle magnitude is 6.8 degrees, with yaw probabilities extending from -20 degrees to +20 degrees. The yaw of greatest probability is, surprisingly, 0 degrees.

I've not seen any experimental data which contradicts this conclusion. But I look forward to seeing what comes across the forums, as this subject has gotten plenty of attention as wind tunnel testing becomes more popular.