yaw angle: modeling wind speed
First Tour magazine, and now VeloNews have published wind tunnel data on "aerodynamic" mass‒start bikes. Each measured the bikes over yaw angles from 0 to 20 degrees, and each averaged over measured angles. Tour measured at 0, 5, 10, and 20 degrees, which implicitly gave uniform weight to the ‒12.5 to +12.5 degree yaw range, then a reduced weight to yaws out to at least ‒20 and +20 degrees. VeloNews tested at uniform intervals across the range from ‒20 to 20 degrees.
Zipp reports, via NY Velocity, that the measured yaw distribution has peaks at around +/‒ 13 degrees, with peak extending (depending on conditions and rider speed) from 7 to 15 degrees, as measured at the head tube. So does this make sense? I thought so, but I wanted to do an analytic analysis of the problem. If wind is varying in speed, and the rider is varying in his heading, averaged over time what relative yaw angle is expected? Worth a quick calculation, I figured.
Unfortunately my "quick calculation" become borderline obsession, and more train commutes than I would ever care to admit become consumed with line after line of algebra. And since I have an enormous algabreic error rate, every minute in derivation was followed by at least five tracking down errors in that derivation.
Ah, well. Hopefully I've gotten this out of my system. I'll start with the wind speed...
For non‒interacting particles at a given temperature, the distribution of kinetic energies is well describned by the Boltzmann distribution. Since kinetic energy is proportional to the square of the magnitude of velocity, and since potential energy at a given altitude is fixed, this results in a velocity distribution described by the Maxwell distribution: velocities are distributed with a normal (Gaussian) distribution in the available velocity space. It's tempting to calculate kinetic energies, and therefore the distribution, using the mass of an N₂ molecule. However, this would be a mistake: it is how you calculate air pressure, or the speed of sound. Wind is instead the average speed of a huge number of particles, not determined by the random fluctuation of individual particle speeds, but rather from macroscopic temperature gradients. If you were to average the randomized isothermal velocities of gas molecules hitting a rider, you'd get very close to zero. Consider Brownian motion, in which a minute dust particle floats slowly and randomly through the air due to the randomized collisions with gas molecules, is an average over an area around 10⁸ smaller. But I'm digressing...
I assume the velocity at a 10 meter reference elevation is distributed with an empirical distribution which represents a Maxwell distribution but with an empirical threshold speed, rather than with an explicit temperature dependence. I then assume at the height most relevant to bicycle aerodynamics, where the wind is more influenced by its interactions with fixed bodys on the ground, topography, people, etc, it is still described by a Maxwellian distribution. Close to the surface of the Earth the wind is constrained to blow primarily parallel to the surface, so I include only velocity components parallel to the ground:
P(v) = P0 exp[‒ (vx² + vy²) / ( 2 v0² ) ] ,
where P0 = 1 / (2 π v0²) is a normalization constant. It has units 1/speed² since P(v) is a two‒dimensional distribution.
Whichever direction the bike is pointing, I'll call that direction x, with an orthogonal direction y. Then as long as the wind speed is always much less than the bike speed, I assume vx is unimportant to the relative wind, and only vy matters. However, this is not generally the case: wind speeds are significant in comparison to the bike speed, which is why it's harder to ride in a cross or headwind than in still air.
So I'll calculate the probability distribution of the magnitude of the wind speed. To do that, I need to recognize that the wind vector in any direction can contribute. The "number" of velocities which can contribute to a given |velocity|² is proportional to the diameter of a circle of radius |velocity|. So I get:
P(|v|) = 2 π |v| P0 exp[‒ |v|² / ( 2 v0² ) ] ,
or plugging in the value of P0:
P(|v|) = ( |v| / v0² ) exp[‒ |v|² / ( 2 v0² ) ].
If I integrate this from 0 to ∞ I'd better get one.... I can see by inspection that this function on the right is the derivative of ‒exp[‒ |v|² / ( 2 v0² ) ], so I do in fact get one for that integral.
One thing that's immediately obvious from this distribution is there is a peak at non‒zero wind speed: differentiate the function, set the polynomial pre‒factor to zero, and you see that the maximum is at |v| = v0.
So what to choose for P0? I've addressed this in a previous post, but I will summarize my simplistic assumptions here. Suppose the "meterilogical" wind (at 10 metere reference elevation, or at 3 meter reference elevation from an unobstructed position, the latter which I assume is similar to a typical 10 meter position) is characterized by v0 = 10 mph. The wheels extend from a height of 0 to approximately 67 cm, and the frame extends from approximately 26 cm to around 82 cm (to the top of the head tube) or to maybe 90 cm if I'm including the seat tube. Since I don't know any better, I use the Hellman formula:
(v / v10) = (h / 10 meters)α,
where v10 is the wind speed at 10 meters, and v is the wind speed at the desired altitude. This model roughly applies up to a few hundred meters above the ground. For "neutral air above human inhabited areas", which I think describes much bike racing, α = 0.34 is recommended. So if I want to evaluate the average of the square of the wind speed from 0.26 meters to 0.9 meters, I integrate (z / 10 meters)0.68 from 0.026 to 0.09 and divide by (0.09 ‒ 0.026), then take the square root, yielding 0.38. For the wheels, I get 0.31. So for the frame, the characteristic wind speed for the frame is around 3.8 mph, which is 1.69 meters/second. Or, for the wheels, I get 1.39 meters/second. Averaging from the ground to the top of the seatpost is 1.52 meters/second.
An illustration of typical yaw angles along the height of the bike, assuming 20 degree yaw at 10 meter elevation, is shown in this plot,
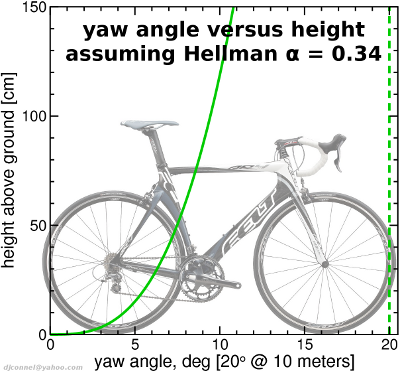
For the rest of these calculations, I assumed 3.6 mph for v0 at the bike level. This is "in the ballpark" of these other estimates. When I derived that number, I assumed the seatpost was a reduced influence. In any case, applying much precision to this estimate is rather absurd, since I'm making crude assumptions in the application of Hellman's formula. But you've got to start somewhere...
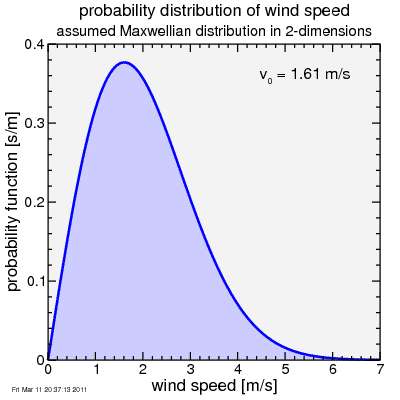
Anyway, here's what I get when I use that value. The probability for wind speeds increases from zero, then it peaks out at 1.61 m/sec, then it quickly decays until by 7 meters/second it is essentially zero on this linear scale.
None of this considers the direction the rider is moving. It could be against the wind, with the wind, perpendicular to the wind, or somewhere in between. I'll look at that next time.
Zipp reports, via NY Velocity, that the measured yaw distribution has peaks at around +/‒ 13 degrees, with peak extending (depending on conditions and rider speed) from 7 to 15 degrees, as measured at the head tube. So does this make sense? I thought so, but I wanted to do an analytic analysis of the problem. If wind is varying in speed, and the rider is varying in his heading, averaged over time what relative yaw angle is expected? Worth a quick calculation, I figured.
Unfortunately my "quick calculation" become borderline obsession, and more train commutes than I would ever care to admit become consumed with line after line of algebra. And since I have an enormous algabreic error rate, every minute in derivation was followed by at least five tracking down errors in that derivation.
Ah, well. Hopefully I've gotten this out of my system. I'll start with the wind speed...
For non‒interacting particles at a given temperature, the distribution of kinetic energies is well describned by the Boltzmann distribution. Since kinetic energy is proportional to the square of the magnitude of velocity, and since potential energy at a given altitude is fixed, this results in a velocity distribution described by the Maxwell distribution: velocities are distributed with a normal (Gaussian) distribution in the available velocity space. It's tempting to calculate kinetic energies, and therefore the distribution, using the mass of an N₂ molecule. However, this would be a mistake: it is how you calculate air pressure, or the speed of sound. Wind is instead the average speed of a huge number of particles, not determined by the random fluctuation of individual particle speeds, but rather from macroscopic temperature gradients. If you were to average the randomized isothermal velocities of gas molecules hitting a rider, you'd get very close to zero. Consider Brownian motion, in which a minute dust particle floats slowly and randomly through the air due to the randomized collisions with gas molecules, is an average over an area around 10⁸ smaller. But I'm digressing...
I assume the velocity at a 10 meter reference elevation is distributed with an empirical distribution which represents a Maxwell distribution but with an empirical threshold speed, rather than with an explicit temperature dependence. I then assume at the height most relevant to bicycle aerodynamics, where the wind is more influenced by its interactions with fixed bodys on the ground, topography, people, etc, it is still described by a Maxwellian distribution. Close to the surface of the Earth the wind is constrained to blow primarily parallel to the surface, so I include only velocity components parallel to the ground:
P(v) = P0 exp[‒ (vx² + vy²) / ( 2 v0² ) ] ,
where P0 = 1 / (2 π v0²) is a normalization constant. It has units 1/speed² since P(v) is a two‒dimensional distribution.
Whichever direction the bike is pointing, I'll call that direction x, with an orthogonal direction y. Then as long as the wind speed is always much less than the bike speed, I assume vx is unimportant to the relative wind, and only vy matters. However, this is not generally the case: wind speeds are significant in comparison to the bike speed, which is why it's harder to ride in a cross or headwind than in still air.
So I'll calculate the probability distribution of the magnitude of the wind speed. To do that, I need to recognize that the wind vector in any direction can contribute. The "number" of velocities which can contribute to a given |velocity|² is proportional to the diameter of a circle of radius |velocity|. So I get:
P(|v|) = 2 π |v| P0 exp[‒ |v|² / ( 2 v0² ) ] ,
or plugging in the value of P0:
P(|v|) = ( |v| / v0² ) exp[‒ |v|² / ( 2 v0² ) ].
If I integrate this from 0 to ∞ I'd better get one.... I can see by inspection that this function on the right is the derivative of ‒exp[‒ |v|² / ( 2 v0² ) ], so I do in fact get one for that integral.
One thing that's immediately obvious from this distribution is there is a peak at non‒zero wind speed: differentiate the function, set the polynomial pre‒factor to zero, and you see that the maximum is at |v| = v0.
So what to choose for P0? I've addressed this in a previous post, but I will summarize my simplistic assumptions here. Suppose the "meterilogical" wind (at 10 metere reference elevation, or at 3 meter reference elevation from an unobstructed position, the latter which I assume is similar to a typical 10 meter position) is characterized by v0 = 10 mph. The wheels extend from a height of 0 to approximately 67 cm, and the frame extends from approximately 26 cm to around 82 cm (to the top of the head tube) or to maybe 90 cm if I'm including the seat tube. Since I don't know any better, I use the Hellman formula:
(v / v10) = (h / 10 meters)α,
where v10 is the wind speed at 10 meters, and v is the wind speed at the desired altitude. This model roughly applies up to a few hundred meters above the ground. For "neutral air above human inhabited areas", which I think describes much bike racing, α = 0.34 is recommended. So if I want to evaluate the average of the square of the wind speed from 0.26 meters to 0.9 meters, I integrate (z / 10 meters)0.68 from 0.026 to 0.09 and divide by (0.09 ‒ 0.026), then take the square root, yielding 0.38. For the wheels, I get 0.31. So for the frame, the characteristic wind speed for the frame is around 3.8 mph, which is 1.69 meters/second. Or, for the wheels, I get 1.39 meters/second. Averaging from the ground to the top of the seatpost is 1.52 meters/second.
An illustration of typical yaw angles along the height of the bike, assuming 20 degree yaw at 10 meter elevation, is shown in this plot,

For the rest of these calculations, I assumed 3.6 mph for v0 at the bike level. This is "in the ballpark" of these other estimates. When I derived that number, I assumed the seatpost was a reduced influence. In any case, applying much precision to this estimate is rather absurd, since I'm making crude assumptions in the application of Hellman's formula. But you've got to start somewhere...

Anyway, here's what I get when I use that value. The probability for wind speeds increases from zero, then it peaks out at 1.61 m/sec, then it quickly decays until by 7 meters/second it is essentially zero on this linear scale.
None of this considers the direction the rider is moving. It could be against the wind, with the wind, perpendicular to the wind, or somewhere in between. I'll look at that next time.

Comments