yaw angle: the effect of relative wind direction
The last time I came up with a proposed distribution of wind speeds at the bike's level. This was based on an assumed relation between wind speed and height, which is for urbanized areas. It doesn't apply to open coastlines, but then it doesn't apply to dense forests, either: just an attempt to model truly "typical" conditions.
But next I need to consider that the bike may be moving in any direction relative to the wind. I assume all headings relative to the wind are equally likely. Each contributes equally to the final net yaw probability distribution.
I'll start by assuming the bike is moving at a constant speed and constant direction, and the wind is also at a constant speed and constant direction. I'll worry about probability functions later.
To go from wind speed |v| to yaw, I add a parameter Φ, the relative angle between the rider's heading (at speed s) and the wind direction. Then I get two components of the relative wind, one parallel to the direction of motion, the other perpendicular. I'll call these relative wind components wu and wv, where wu is the relative head‒wind in the direction of travel, and wv is the cross‒wind:
wu = |v| cos Φ + s ,
wv = |v| sin Φ .
The tangent of the yaw angle is then the ratio (the sign is arbitrary):
tan yaw = |v| sin Φ / ( |v| cos Φ + s ) .
I plot that result here:
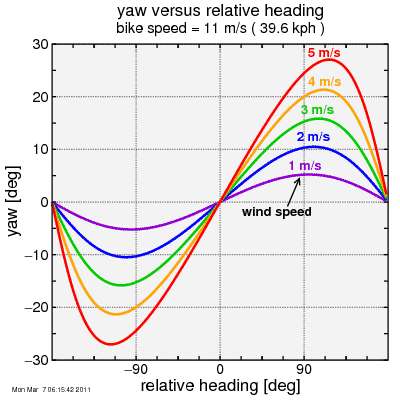
For each value of wind speed, there is a maximum yaw magnitude, the maximum higher the higher the ratio of wind speed to bike speed.
If I consider Φ to be a random variable equally distributed over all angles in the unit circle, I can calculate a probability distribution for yaw, given |v| and |s|.
First I take the derivative of the tangent of yaw:
d tan yaw / d Φ =
|v| cos Φ / ( |v| cos Φ + s ) + |v²| sin² Φ / ( |v| cos Φ + s )² =
( |v|² cos² Φ + s |v| cos Φ + |v²| sin² Φ ) / ( |v| cos Φ + s )² =
|v| ( s cos Φ + |v|) / ( |v| cos Φ + s )²
I want the derivative of yaw, not the derivative of the tangent of yaw, so I use:
d tan yaw = dyaw ( 1 + tan² yaw )
or
d yaw = d tan yaw / ( 1 + tan² yaw )
which yields:
d yaw / d Φ =
|v| ( s cos Φ + |v|) / [ ( |v| cos Φ + s )² ( 1 + |v|² sin² Φ / ( |v| cos Φ + s )² ) ] =
|v| ( s cos Φ + |v|) / [ ( |v| cos Φ + s )² + |v|² sin² Φ ] =
|v| ( s cos Φ + |v|) / ( |v|² cos² Φ + 2 s |v| cos Φ + s² + |v|² sin² Φ ) =
|v| ( s cos Φ + |v|) / ( |v|² + 2 s |v| cos Φ + s² )
Sanity checks:
if |v| = 0, s > 0: d yaw / d Φ = 0 (this is correct: yaw is always 0 if there's no wind).
If s = 0, |v| > 0: d yaw / d Φ = 1 (this is correct: yaw = Φ if the bike isn't moving).
So it passes these checks.
Another interesting case:
if s = |v|: d yaw / d Φ = 1/2 (yaw = Φ / 2)
If the rider is going the same speed as the wind, the yaw angle is half the difference of the rider's direction and the wind direction up to the point the rider is moving with the wind, in which case net wind is zero and the wind direction is no longer uniquely defined.
To be continued...
But next I need to consider that the bike may be moving in any direction relative to the wind. I assume all headings relative to the wind are equally likely. Each contributes equally to the final net yaw probability distribution.
I'll start by assuming the bike is moving at a constant speed and constant direction, and the wind is also at a constant speed and constant direction. I'll worry about probability functions later.
To go from wind speed |v| to yaw, I add a parameter Φ, the relative angle between the rider's heading (at speed s) and the wind direction. Then I get two components of the relative wind, one parallel to the direction of motion, the other perpendicular. I'll call these relative wind components wu and wv, where wu is the relative head‒wind in the direction of travel, and wv is the cross‒wind:
wu = |v| cos Φ + s ,
wv = |v| sin Φ .
The tangent of the yaw angle is then the ratio (the sign is arbitrary):
tan yaw = |v| sin Φ / ( |v| cos Φ + s ) .
I plot that result here:

For each value of wind speed, there is a maximum yaw magnitude, the maximum higher the higher the ratio of wind speed to bike speed.
If I consider Φ to be a random variable equally distributed over all angles in the unit circle, I can calculate a probability distribution for yaw, given |v| and |s|.
First I take the derivative of the tangent of yaw:
d tan yaw / d Φ =
|v| cos Φ / ( |v| cos Φ + s ) + |v²| sin² Φ / ( |v| cos Φ + s )² =
( |v|² cos² Φ + s |v| cos Φ + |v²| sin² Φ ) / ( |v| cos Φ + s )² =
|v| ( s cos Φ + |v|) / ( |v| cos Φ + s )²
I want the derivative of yaw, not the derivative of the tangent of yaw, so I use:
d tan yaw = dyaw ( 1 + tan² yaw )
or
d yaw = d tan yaw / ( 1 + tan² yaw )
which yields:
d yaw / d Φ =
|v| ( s cos Φ + |v|) / [ ( |v| cos Φ + s )² ( 1 + |v|² sin² Φ / ( |v| cos Φ + s )² ) ] =
|v| ( s cos Φ + |v|) / [ ( |v| cos Φ + s )² + |v|² sin² Φ ] =
|v| ( s cos Φ + |v|) / ( |v|² cos² Φ + 2 s |v| cos Φ + s² + |v|² sin² Φ ) =
|v| ( s cos Φ + |v|) / ( |v|² + 2 s |v| cos Φ + s² )
Sanity checks:
if |v| = 0, s > 0: d yaw / d Φ = 0 (this is correct: yaw is always 0 if there's no wind).
If s = 0, |v| > 0: d yaw / d Φ = 1 (this is correct: yaw = Φ if the bike isn't moving).
So it passes these checks.
Another interesting case:
if s = |v|: d yaw / d Φ = 1/2 (yaw = Φ / 2)
If the rider is going the same speed as the wind, the yaw angle is half the difference of the rider's direction and the wind direction up to the point the rider is moving with the wind, in which case net wind is zero and the wind direction is no longer uniquely defined.
To be continued...

Comments