2010 Low-Key Hillclimbs consistency ranking
I wanted to do a ranking for consistency: whose scores are the most similar week-to-week.
Until this year this wasn't really possible. In the women, since the numbers would typically be relatively small and since scores were proportional to the median time of all women, if a faster group showed up everyone's score would tend to be lower, and if a slower group showed everyone's score tended to be higher. As a result you could ride exactly the same each week and still get a more variable score than someone riding less consistently. And in the hybrid-electric category since turn-out was typically one, Bill Bushnell would lock down exactly 100 points each week: perfectly consistent!
But with the change this year to using gender-corrected times and a median taken from the combined rider population (Excluding tandems), the median itself should be more consistent, and a consistency ranking becomes more meaningful.
So I had to come up with a formula. The obvious thing is to take the statistical standard deviation of a rider's scores. But I clearly don't want to use the score itself: if a rider is faster, the score will be higher, and a 1% variation in speed represents a larger variation in score than a 1% variation in a slower rider's speed. Or, if I used time,the opposite problem would occur: a 1% variation of a slower rider's time is greater than a 1% variation in a faster rider's time. So I take the logarithm (the natural logarithm, but that's not important) of each rider's score, treat scores as samples from a static probability distribution, and calculate the estimate of the standard deviation. Given a set of values zi, each the natural logarithm of a rider's score from a particular climb (excluding tandem weeks and scores assigned for volunteering), the estimate S of the standard deviation is:
S2 = ( s2 - s12 / N ) / (N - 1),
where s1 is the sum over i of z, and s2 is the sum over i of z2.
But this isn't quite good enough. The reason is that a rider might show up and do a small number of climbs and get lucky, having the scores happen to turn out close to each other, but maintaining luck through up to the full nine-climb series is far more challenging. So to account for this I look at the standard error in the estimator of the standard deviation. Using not the estimator itself, but a value two standard errors larger than the estimator, increases the confidence that someone scoring well in the ranking was truly being consistent, and wasn't simply lucky to have gotten a similar result in a small number of climbs. It "rewards" riders who do more climbs, producing a statistically significant set of scores from which to derive the ranking.
The stsndard error of the estimate of the standard deviation Eσ is:
Eσ = sqrt [ 2 / ( N - 1 ) ] σ,
where N is the number of samples and σ is the true standard deviation. So if I use S for σ and add this on to S I get my score:
S + 2 Eσ = sqrt[ ( s2 - s1 / N ) / (N - 1) ] × [ 1 + sqrt [ 8 / ( N - 1 ) ] ].
A problem with this is that S may not be a good estimate of σ, so if a rider gets "lucky", I'm underestimating Eσ as well as σ. Ah, well: it's just a hillclimb ranking. At least this approach acknowledges that it's harder to be consistent over a large number of rides than it is over a small number.
Here's a plot of this scale factor applied to the standard deviation estimate:
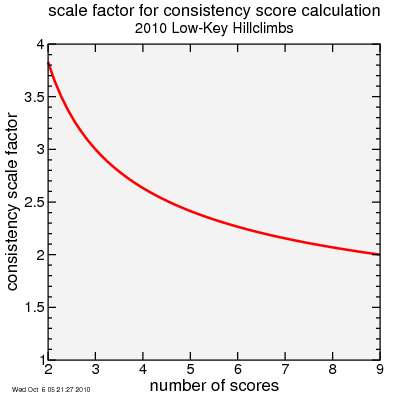
Finally, I multiply this score by 100 when I publish the rankings, to give numbers more in the 1-100 range that people tend to prefer.
Warning: I change this formula slightly in the next blog post...
Until this year this wasn't really possible. In the women, since the numbers would typically be relatively small and since scores were proportional to the median time of all women, if a faster group showed up everyone's score would tend to be lower, and if a slower group showed everyone's score tended to be higher. As a result you could ride exactly the same each week and still get a more variable score than someone riding less consistently. And in the hybrid-electric category since turn-out was typically one, Bill Bushnell would lock down exactly 100 points each week: perfectly consistent!
But with the change this year to using gender-corrected times and a median taken from the combined rider population (Excluding tandems), the median itself should be more consistent, and a consistency ranking becomes more meaningful.
So I had to come up with a formula. The obvious thing is to take the statistical standard deviation of a rider's scores. But I clearly don't want to use the score itself: if a rider is faster, the score will be higher, and a 1% variation in speed represents a larger variation in score than a 1% variation in a slower rider's speed. Or, if I used time,the opposite problem would occur: a 1% variation of a slower rider's time is greater than a 1% variation in a faster rider's time. So I take the logarithm (the natural logarithm, but that's not important) of each rider's score, treat scores as samples from a static probability distribution, and calculate the estimate of the standard deviation. Given a set of values zi, each the natural logarithm of a rider's score from a particular climb (excluding tandem weeks and scores assigned for volunteering), the estimate S of the standard deviation is:
S2 = ( s2 - s12 / N ) / (N - 1),
where s1 is the sum over i of z, and s2 is the sum over i of z2.
But this isn't quite good enough. The reason is that a rider might show up and do a small number of climbs and get lucky, having the scores happen to turn out close to each other, but maintaining luck through up to the full nine-climb series is far more challenging. So to account for this I look at the standard error in the estimator of the standard deviation. Using not the estimator itself, but a value two standard errors larger than the estimator, increases the confidence that someone scoring well in the ranking was truly being consistent, and wasn't simply lucky to have gotten a similar result in a small number of climbs. It "rewards" riders who do more climbs, producing a statistically significant set of scores from which to derive the ranking.
The stsndard error of the estimate of the standard deviation Eσ is:
Eσ = sqrt [ 2 / ( N - 1 ) ] σ,
where N is the number of samples and σ is the true standard deviation. So if I use S for σ and add this on to S I get my score:
S + 2 Eσ = sqrt[ ( s2 - s1 / N ) / (N - 1) ] × [ 1 + sqrt [ 8 / ( N - 1 ) ] ].
A problem with this is that S may not be a good estimate of σ, so if a rider gets "lucky", I'm underestimating Eσ as well as σ. Ah, well: it's just a hillclimb ranking. At least this approach acknowledges that it's harder to be consistent over a large number of rides than it is over a small number.
Here's a plot of this scale factor applied to the standard deviation estimate:

Finally, I multiply this score by 100 when I publish the rankings, to give numbers more in the 1-100 range that people tend to prefer.
Warning: I change this formula slightly in the next blog post...

Comments