Chris Horner on Sierra Road: power, speed, and equivalent Old La Honda time
After much speculation and indirect guessing, I finally got a time for Chris Horner climbing Sierra Road during stage 4 of the 2011 Amgen Tour of California.

Recovox News
VeloNews posted Rory Sutherland's power data, with analysis, for the climb. Rory started the climb in Horner's group and finished 1:15 behind. According to the article, Sutherland's time was an impressive 18:02. However that puts Horner's time at an amazing 16:47. I'd put maybe 2-second error bars on that number. For example, if Sutherland hit the base of the climb one second after Horner, then Horner's time would be one second longer. But I'll stick with this estimate.
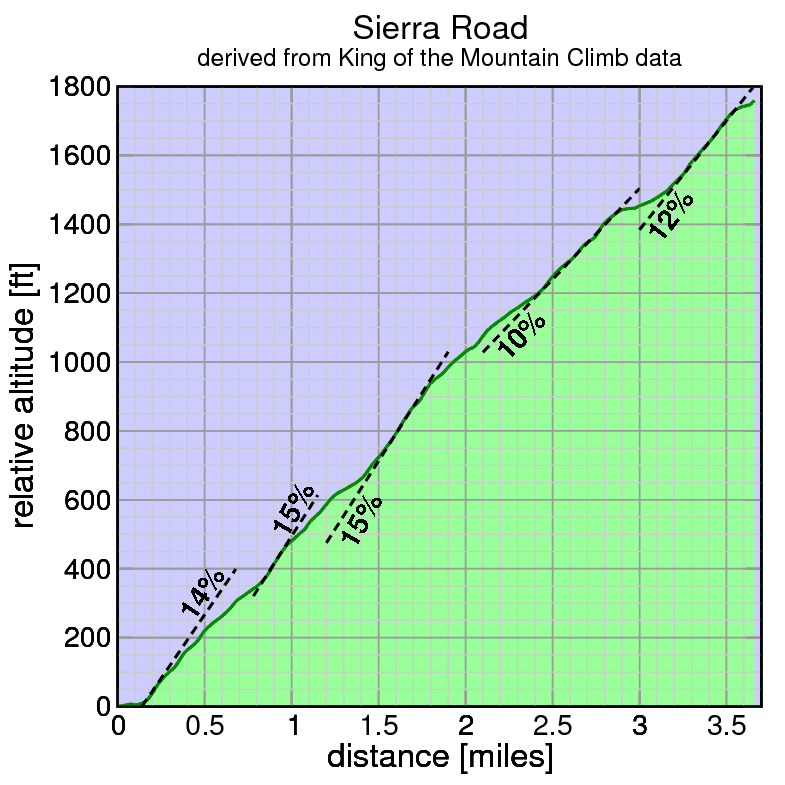
Sierra Road climbs 536 meters according to my numbers. So plugging that into Chris Horner's 0.280 hour ride and you get a VAM of 1916. Generally in the Tour de France if you see a VAM in excess of 1700 that's extraordinary. 1916?
But in addition to overcoming gravity when you climb (producing VAM) you're also pushing aside air (wind resistance) and rubber (rolling resistance). The steeper the climb, the less distance traveled, and the less wind and rubber you need to move. That leaves more power for moving upward. And while there are climbs as steep as Sierra in the Giro d'Italia, in the Tour such grades are rare. Additionally, the riders had come off a rest day (the canceled first stage) and a downhill stage ending in a brief circuit race. He was fresh as can be, with the exception of having climbed the backside of Mt Hamilton as "warm-up", but compared to a typical "Grand Tour" Queen stage that relatively short climb is only a minor inconvenience.
We could guess at how much power it took Horner to climb at this rate, but ther'es no need: Rory Sutherland's data is an average of 6.1 W/kg. If I assume climbing rate is proportional to W/kg (a decent approximation) I get 6.55 W/kg for Horner.
Horner posted a low-resolution plot of his power data on-line. He started at around 450 watts, dropped off to around 400 watts, then ramped it up to 420 watts by the finish. If I assume a body mass of 65 kg ( 143 lb), I get 426 watts. So this is consistent.
To check this, I make a few assumptions. His bike is exactly 6.8 kg (the UCI limit) but add in another 1.5 kg of clothing, shoes, helmet, etc (the stuff adds up: weigh it sometime). Then I assume that the rolling resistance coefficient is around 0.3% (the pavement was very good) and drivetrain efficiency is 97%. I get 6.37 W/kg. That leaves 72 watts for wind resistance. He was climbing at 5.59 meters/second, and assuming an air density of 1.1 kg/m³ (a guess) I get a CdA of only 0.32, which is precisely what Tour magazine measured for a "typical" rider on a Cannondale road bike.
The canonical number which comes to mind of the benefits of supplementation in the Armstrong era is Michele Ferrari's target threshold for winning the tour de France of 6.7 W/kg (from Lance Armstrong's War by Coyle). Coggan's "functional threshold power" (which tends to be slightly higher, I believe than the blood-lactate-based number used by Ferrari) is the power a rider can sustain for an hour. A standard estimate of the power you can sustain for an hour is to ride for 20 minutes then subtract either 5% (Hunter Allen) or 7% (Joe Friel) from the result. I assume Horner has excellent aerobic endurance so I'll assume 5%. To go from 20 minutes down to 16:47 I'll use the critical power model with AWC/CP = 90 seconds (a typical number). The result is that his FTP can be estimated as 93.7% of the power he was able to ride for 16:47, under ideal conditions.
So this results in an estimate of 6.14 W/kg for Horner's FTP. He thus falls well short of a number required to win the Tour in the age of Armstrong, Hamilton, Landis, and Hincapie. And that's a good thing.
The next question: what would he do for Old La Honda Road? It requires a self-consistent calculation: we know what he can average for 16:47, we have a formula for predicting what he can average for shorter times (the critical power model), so if we know how long it takes to climb OLH we can estimate how much power he could deliver there. But we need to know the power to estimate the time, so it's simplest to use an iterative calculation.
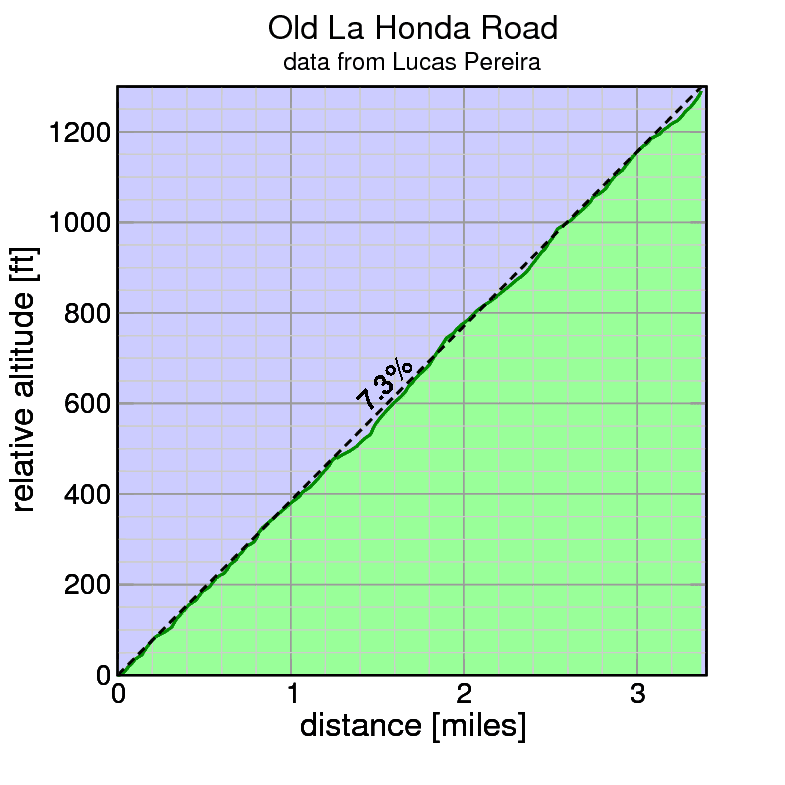
Old La Honda climbs 393 meters in 5.42 km. I'll assume a CdA of 0.32 (typical of what was measured by Tour magazine with a dummy) with an air density of 1.15 kg/m². I'll assume a 0.5% coefficient of rolling resistance as Old La Honda has mixed pavement quality. I'll still assume a 0.97 drivetrain efficiency. Playing around with the numbers I get 13.70 minutes = 13:41.
That would be a record, but only by 17 seconds or so. Greg Drake told me he'd done "sub-14", and it's rumored Eric Wohlberg was even faster. So Horner had a great ride, no question, especially for a master's racer, but the result isn't as insane as it might appear just from the VAM.
Take 4 lb off the UCI-limited bike, drop the bottle cages, pump the tires up to 140-160 psi, and get a more restrained warm-up than blasting over Mines Road and I think it's safe to say Horner could knock 30 seconds off that time.

Recovox News
VeloNews posted Rory Sutherland's power data, with analysis, for the climb. Rory started the climb in Horner's group and finished 1:15 behind. According to the article, Sutherland's time was an impressive 18:02. However that puts Horner's time at an amazing 16:47. I'd put maybe 2-second error bars on that number. For example, if Sutherland hit the base of the climb one second after Horner, then Horner's time would be one second longer. But I'll stick with this estimate.

Sierra Road climbs 536 meters according to my numbers. So plugging that into Chris Horner's 0.280 hour ride and you get a VAM of 1916. Generally in the Tour de France if you see a VAM in excess of 1700 that's extraordinary. 1916?
But in addition to overcoming gravity when you climb (producing VAM) you're also pushing aside air (wind resistance) and rubber (rolling resistance). The steeper the climb, the less distance traveled, and the less wind and rubber you need to move. That leaves more power for moving upward. And while there are climbs as steep as Sierra in the Giro d'Italia, in the Tour such grades are rare. Additionally, the riders had come off a rest day (the canceled first stage) and a downhill stage ending in a brief circuit race. He was fresh as can be, with the exception of having climbed the backside of Mt Hamilton as "warm-up", but compared to a typical "Grand Tour" Queen stage that relatively short climb is only a minor inconvenience.
We could guess at how much power it took Horner to climb at this rate, but ther'es no need: Rory Sutherland's data is an average of 6.1 W/kg. If I assume climbing rate is proportional to W/kg (a decent approximation) I get 6.55 W/kg for Horner.
Horner posted a low-resolution plot of his power data on-line. He started at around 450 watts, dropped off to around 400 watts, then ramped it up to 420 watts by the finish. If I assume a body mass of 65 kg ( 143 lb), I get 426 watts. So this is consistent.
To check this, I make a few assumptions. His bike is exactly 6.8 kg (the UCI limit) but add in another 1.5 kg of clothing, shoes, helmet, etc (the stuff adds up: weigh it sometime). Then I assume that the rolling resistance coefficient is around 0.3% (the pavement was very good) and drivetrain efficiency is 97%. I get 6.37 W/kg. That leaves 72 watts for wind resistance. He was climbing at 5.59 meters/second, and assuming an air density of 1.1 kg/m³ (a guess) I get a CdA of only 0.32, which is precisely what Tour magazine measured for a "typical" rider on a Cannondale road bike.
The canonical number which comes to mind of the benefits of supplementation in the Armstrong era is Michele Ferrari's target threshold for winning the tour de France of 6.7 W/kg (from Lance Armstrong's War by Coyle). Coggan's "functional threshold power" (which tends to be slightly higher, I believe than the blood-lactate-based number used by Ferrari) is the power a rider can sustain for an hour. A standard estimate of the power you can sustain for an hour is to ride for 20 minutes then subtract either 5% (Hunter Allen) or 7% (Joe Friel) from the result. I assume Horner has excellent aerobic endurance so I'll assume 5%. To go from 20 minutes down to 16:47 I'll use the critical power model with AWC/CP = 90 seconds (a typical number). The result is that his FTP can be estimated as 93.7% of the power he was able to ride for 16:47, under ideal conditions.
So this results in an estimate of 6.14 W/kg for Horner's FTP. He thus falls well short of a number required to win the Tour in the age of Armstrong, Hamilton, Landis, and Hincapie. And that's a good thing.

The next question: what would he do for Old La Honda Road? It requires a self-consistent calculation: we know what he can average for 16:47, we have a formula for predicting what he can average for shorter times (the critical power model), so if we know how long it takes to climb OLH we can estimate how much power he could deliver there. But we need to know the power to estimate the time, so it's simplest to use an iterative calculation.
Old La Honda climbs 393 meters in 5.42 km. I'll assume a CdA of 0.32 (typical of what was measured by Tour magazine with a dummy) with an air density of 1.15 kg/m². I'll assume a 0.5% coefficient of rolling resistance as Old La Honda has mixed pavement quality. I'll still assume a 0.97 drivetrain efficiency. Playing around with the numbers I get 13.70 minutes = 13:41.
That would be a record, but only by 17 seconds or so. Greg Drake told me he'd done "sub-14", and it's rumored Eric Wohlberg was even faster. So Horner had a great ride, no question, especially for a master's racer, but the result isn't as insane as it might appear just from the VAM.
Take 4 lb off the UCI-limited bike, drop the bottle cages, pump the tires up to 140-160 psi, and get a more restrained warm-up than blasting over Mines Road and I think it's safe to say Horner could knock 30 seconds off that time.

Comments
Hopefully I'll get over to you guys some time during race season (and when I'm light) to get a good time up for the climb.
How much did the drafting help for the first few minutes though?
I'd love to do an OLH behind a moto - at 24kmph around 12-14% advantage?
OLH motorpacing: that's a good idea!
It's a difference between large numbers issue, but the CdA is low for Sutherland on Sierra in part because he was drafting part of the way. But given the wind, I don't think a meaningful estimate can be gained for how much drafting helped. I think 1-2% is typical for fast climbers on OLH. It's inversely proportional to grade-squared so in still air you'd expect around 60% as much benefit on Sierra. So it's hard to believe unless there's a head or crosswind that drafting the first minute saved more than 2 seconds on Sierra.
CH stated only AC can beat him ATM on climbs
I redid the calculation of Contador's CdA on Sierra assuming a 0.3% Crr, which seems more reasonable on the good pavement with pro-level tubular tires. The CdA comes out right where you'd expect it. Old La Honda has rougher pavement so maybe I'll stick with the 0.5% number there.