total climbing and descending algorithm
Last time I described how the goal was to eliminate climbs less than some threshold (which I'll call hmin) while preserving the starting and ending altitude for a route. Here's the algorithm I implemented.
A climb is represented as a series of points, each with a distance and altitude. I'll ignore distance. Distance might be used to apply some numerical smoothing to the data before implementing this algorithm, but that's optional. Here I care only about altitude.
One approach might be to consider consecutive points and count only climbing or descending which exceeds hmin. This obviously fails because a climb might consist of 1000 consecutive one-meter altitude gains. So then I might combine all adjacent non-descending segments together, then all adjacent non-climbing segments, etc, to yield alternating climb-descend-climb-descend. I could then eliminate the segments which gain or lose less than hmin But this isn't so easy either. Consider a climb which gains 4 meters, descends one, then gains 4, descends 1, one hundred times total. That's a 300 meter climb, and certainly should be counted.
So I've got to be careful in how I do this.
I'll look at four consecutive points at a time. I'll call these points a, b, c, and d. If I move on to the next point, the old b becomes the new a, the old c becomes the new b, the old d becomes the new c, and the new d is the point which follows the old d. Additionally, if I delete a point, the following points shift to fill the missing position. For example, if I delete c, the old d becomes the new c, and the point following the old d becomes the new d.
Here's an example derived from randomly-generated numbers.... I'll set hmin = 5. I list altitudes, which could be meters, but that's irrelevant:
38, 26, 23, 20, 46, 42, 44, 29, 8, 41
In each case the point I've been labeling "a" will be marked:
38, 26, 23, 20, 46, 31, 44, 29, 8, 41
First, step 1:
38, 23, 20, 46, 42, 27, 29, 8, 41
38, 20, 46, 42, 27, 29, 8, 41
Step 1 now is done, because 20 < 38, and 20 < 46. Then step 2 does nothing (since 46 > 20, and 46 > 42). So step 3: 46 ‒ 20 > 5, so I don't delete any points, and move on to the next point: 38, 20, 46, 42, 27, 29, 8, 41
Step 1: I'm not at the first position, so I skip this.
Step 2: 46 > 42 > 27, so 42 goes
38, 20, 46, 27, 29, 8, 41
Step 3: 46 ‒ 20 > 5, so I don't delete anything and move ahead (step 4):
38, 20, 46, 27, 29, 8, 41
Step 1: Not at the first position, so not needed.
Step 2: 29 is the largest of 27, 29, and 8, so nothing to delete here.
Step 3: 29 ‒ 27 < 2, so I need to delete the pair 27, 29:
38, 20, 46, 8, 41
Step 4: we move back a point:
38, 20, 46, 8, 41
Steps 1, 2, and 3 do nothing, so we move the point back up:
38, 20, 46, 8, 41
Step 1: Not needed, since I'm not at the first position.
Step 2: there's no point d, so nothing to do.
Step 3: there's no point d, so nothing to do, and I step forward:
38, 20, 46, 8, 41
I've got only two points left, so I'm done:
38, 20, 46, 8, 41
So I see I have a descent of 18, followed by a climb of 26, then a descent of 38, then finally a climb of 33. Total climbing = 26 + 33 = 59, while total descending = 18 + 38 = 56.
So that's it: really simple.
This example wasn't the best, because it failed to demonstrate why you need to step back after deleting point pairs. The reason is if you delete b and c, then the old d becomes the new b, and it's possible the difference between a and b is now less than the hmin. If I step backward I'll catch that is step 3.
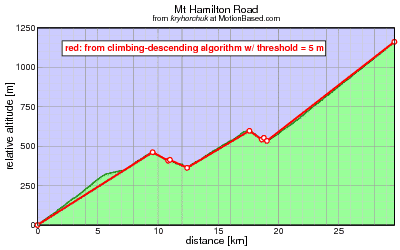
Here's the result for Mt Hamilton Road, using data I got from Garmin Connect:
Here's these key points plotted on top of the original profile:
One comment on this algorithm: it's not totally rational. Consider the following points:
0, 1 .
Total climbing = 1, since I don't touch either the starting or the finishing point. But now I add an additional point:
0, 1, 0 ,
and now total climbing is 0. So adding a point reduced the total climbing. But what can you do? The alternative is total climbing minus total descending might not equal the net altitude change, so I'm willing to live with the anomaly.
A climb is represented as a series of points, each with a distance and altitude. I'll ignore distance. Distance might be used to apply some numerical smoothing to the data before implementing this algorithm, but that's optional. Here I care only about altitude.
One approach might be to consider consecutive points and count only climbing or descending which exceeds hmin. This obviously fails because a climb might consist of 1000 consecutive one-meter altitude gains. So then I might combine all adjacent non-descending segments together, then all adjacent non-climbing segments, etc, to yield alternating climb-descend-climb-descend. I could then eliminate the segments which gain or lose less than hmin But this isn't so easy either. Consider a climb which gains 4 meters, descends one, then gains 4, descends 1, one hundred times total. That's a 300 meter climb, and certainly should be counted.
So I've got to be careful in how I do this.
I'll look at four consecutive points at a time. I'll call these points a, b, c, and d. If I move on to the next point, the old b becomes the new a, the old c becomes the new b, the old d becomes the new c, and the new d is the point which follows the old d. Additionally, if I delete a point, the following points shift to fill the missing position. For example, if I delete c, the old d becomes the new c, and the point following the old d becomes the new d.
- First, if I'm at the first position in the data (otherwise this isn't needed: until b is either higher than both a and c, or lower than both a and c, or until there is no remaining point c, delete b.
- Next, until c is either higher than both b and d, or lower than both b and d, or until there are no remaining point d, delete c.
- If there's still a point d, then if the difference between the altitudes of b and c is less than hmin, then delete both b and c.
- If b and c were deleted, move back a point. Otherwise, move ahead a point.
- If there's still a point c, repeat, otherwise we're done.
Here's an example derived from randomly-generated numbers.... I'll set hmin = 5. I list altitudes, which could be meters, but that's irrelevant:
38, 26, 23, 20, 46, 42, 44, 29, 8, 41
In each case the point I've been labeling "a" will be marked:
38, 26, 23, 20, 46, 31, 44, 29, 8, 41
First, step 1:
38, 23, 20, 46, 42, 27, 29, 8, 41
38, 20, 46, 42, 27, 29, 8, 41
Step 1 now is done, because 20 < 38, and 20 < 46. Then step 2 does nothing (since 46 > 20, and 46 > 42). So step 3: 46 ‒ 20 > 5, so I don't delete any points, and move on to the next point: 38, 20, 46, 42, 27, 29, 8, 41
Step 1: I'm not at the first position, so I skip this.
Step 2: 46 > 42 > 27, so 42 goes
38, 20, 46, 27, 29, 8, 41
Step 3: 46 ‒ 20 > 5, so I don't delete anything and move ahead (step 4):
38, 20, 46, 27, 29, 8, 41
Step 1: Not at the first position, so not needed.
Step 2: 29 is the largest of 27, 29, and 8, so nothing to delete here.
Step 3: 29 ‒ 27 < 2, so I need to delete the pair 27, 29:
38, 20, 46, 8, 41
Step 4: we move back a point:
38, 20, 46, 8, 41
Steps 1, 2, and 3 do nothing, so we move the point back up:
38, 20, 46, 8, 41
Step 1: Not needed, since I'm not at the first position.
Step 2: there's no point d, so nothing to do.
Step 3: there's no point d, so nothing to do, and I step forward:
38, 20, 46, 8, 41
I've got only two points left, so I'm done:
38, 20, 46, 8, 41
So I see I have a descent of 18, followed by a climb of 26, then a descent of 38, then finally a climb of 33. Total climbing = 26 + 33 = 59, while total descending = 18 + 38 = 56.
So that's it: really simple.
This example wasn't the best, because it failed to demonstrate why you need to step back after deleting point pairs. The reason is if you delete b and c, then the old d becomes the new b, and it's possible the difference between a and b is now less than the hmin. If I step backward I'll catch that is step 3.
Here's the result for Mt Hamilton Road, using data I got from Garmin Connect:
km meters climbing descending 0 0 0 0 9.56243 461.522 461.522 0 10.8524 407.685 461.522 53.837 10.9968 413.452 467.289 53.837 12.418 362.502 467.289 104.787 17.5911 597.073 701.86 104.787 18.6179 541.794 701.86 160.066 18.7925 552.852 712.918 160.066 19.0447 533.623 712.918 179.295 29.6209 1161.39 1340.68 179.295
Here's these key points plotted on top of the original profile:

One comment on this algorithm: it's not totally rational. Consider the following points:
0, 1 .
Total climbing = 1, since I don't touch either the starting or the finishing point. But now I add an additional point:
0, 1, 0 ,
and now total climbing is 0. So adding a point reduced the total climbing. But what can you do? The alternative is total climbing minus total descending might not equal the net altitude change, so I'm willing to live with the anomaly.

Comments