total climbing and descending algorithm: FAIL
In my last few blog posts, I proposed a total climbing algorithm. Now to tell the truth, I didn't just invent this for the first time now -- years ago I wrote a program to decode files from the Specialized pBrain, a rather well-designed altitude-recoring cycling computer which actually cost more over 10 years ago than an Edge 500 does today, but having downloadable altitude profiles was so novel, I considered it worth every penny, at least until the bike I had it mounted to was stolen. I lost track of that old source code so I basically started from scratch to facilitate generating climbing statistics for the Low-Key Hillclimbs.
Anyway, I was reviewing the plots I posted last time and I realized the algorithm I just described was flawed. You can see it most clearly in the 50 meter threshold plot:
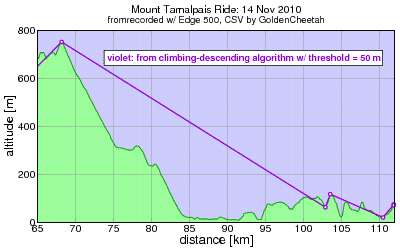
Ouch -- there's a bunch of low-lying fruit which remains unpicked in the 90-95 km range, all passed up for a higher point at km 103. This clearly isn't calculating total climbing properly.
Since the algoritm calculates climbing and descending it had better be the case that climbing calculated in one direction equals descending calculated in the opposite direction, and for that to be the case the points chosen for the tops and bottoms of each sub-climb (or descent) should have the same altitudes. This is clearly not the case here:
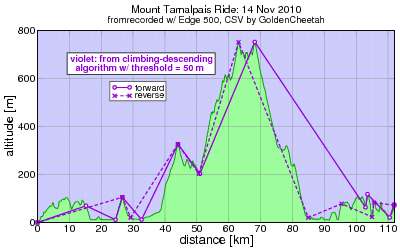
What a total mess: the algorithm is choosing different peak and valley points if it starts from the right than if it starts from the left. Neither of these directions yields the optimal choice. For example there's a big juicy peak at km 9 which neither direction chooses.
The problem is when I had 4 consecutive points and eliminted the middle two (the second of three segments) if it was less than the climbing threshold. Yet I reclessly pruned sub-standard segments without due attention to maximizing the altitude gain of the surviving segment. Consider the following bad example, which if the points are processed left-to-right the algorithm I described would yield:

Bad, bad, bad. The top of that hill has been snipped off. The following is the correct choice:

Once you've got a good picture of what you want, the algorithm almost produces itself. And in this case I got a big deja-vu from having worked on this 10 years ago.
Anyway, the "correct" approach next time...
Anyway, I was reviewing the plots I posted last time and I realized the algorithm I just described was flawed. You can see it most clearly in the 50 meter threshold plot:

Ouch -- there's a bunch of low-lying fruit which remains unpicked in the 90-95 km range, all passed up for a higher point at km 103. This clearly isn't calculating total climbing properly.
Since the algoritm calculates climbing and descending it had better be the case that climbing calculated in one direction equals descending calculated in the opposite direction, and for that to be the case the points chosen for the tops and bottoms of each sub-climb (or descent) should have the same altitudes. This is clearly not the case here:

What a total mess: the algorithm is choosing different peak and valley points if it starts from the right than if it starts from the left. Neither of these directions yields the optimal choice. For example there's a big juicy peak at km 9 which neither direction chooses.
The problem is when I had 4 consecutive points and eliminted the middle two (the second of three segments) if it was less than the climbing threshold. Yet I reclessly pruned sub-standard segments without due attention to maximizing the altitude gain of the surviving segment. Consider the following bad example, which if the points are processed left-to-right the algorithm I described would yield:

Bad, bad, bad. The top of that hill has been snipped off. The following is the correct choice:

Once you've got a good picture of what you want, the algorithm almost produces itself. And in this case I got a big deja-vu from having worked on this 10 years ago.
Anyway, the "correct" approach next time...

Comments
http://softsurfer.com/Archive/algorithm_0205/algorithm_0205.htm
I thought about it a bit on my ride today and it seemed reasonable. I just don't know how you'd compute a rolling total with it, making it less useful.
I'm fine with end-of-ride algorithms, though. There's no reason to constrain end-of-ride to be what can be displayed on-the-fly. Do the best you can with what you have at any given time.
In any case, just wondering. I'll admit, the algorithms are a bit beyond me, but it reads like an interesting project nonetheless. All the best, and of course, don't forget to:
Ride smart, stay safe, have fun.
Sincerely,
DJcontraption
www.twitter.com/djcontraption
Seems like it should be possible to convert pbrain into tcx or gpx format. It's been years since I touched that p-brain code, but I'll try to take a look at it and see if I can hack something together. It should be fairly easy.