Dynamic pressure and barometric altimetry: simulation results
In my last post on the subject of barometric altimetry, it was discussed that a moving altimeter may report a lower altitude than a stationary one, due to the dynamic pressure of the air piling up in front of the moving cyclist. The amount of this altitude increase is determined by a coefficient between zero and one relating the effective wind speed to the cyclist speed.
Before that, I described how I'd combine a barometric altitude signal with a GPS signal to get the best of both: the short-term responsiveness and reliability of the barometric altimeter with the general accuracy of the GPS (at least when there's a signal). I'd applied this to randomly generated data, which were derived using a simple pacing model with the bike power-speed equations.
The effect of dynamic pressure on measured altitude is simply derived from Bernoulli's equation:
Δz = ‒½ ( kdp v )² / g,
where Δz is the error in altitude, v is the speed relative to the wind, kdp is the coefficient dependent on the altimeter position and orientation, and g is the acceleration of gravity.
The the smoothed average of the GPS signal is used to correct for errors in the barometric altimeter, how the dynamic pressure affects the derived altitude with my algorithm depends on how speed fluctuates, not just on the speed. So to account for this, I changed my assumption about power. Instead of a nice steady power, I assumed power fluctuates between 0% and 200% of the "optimal" value, varying sinusoidally with a period which I varied. Furthermore, just to be pedantic, for each period of power I used each of four phases. I did each of these "simulations" for kdp of 0 (no stagnation pressure effect) and 0.5.
Here's the result, where I only averaged over times starting with 100 seconds, to avoid the details of the initial acceleration having too much effect:
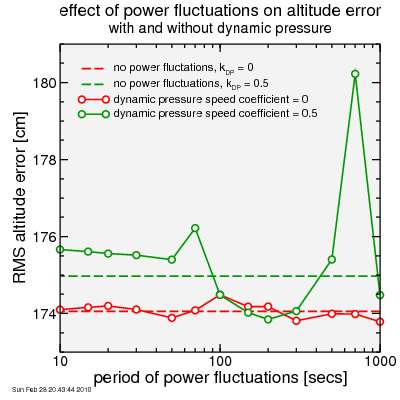
The dotted lines show the result with the smooth power. The oscillating power results are shown by the dots connected by the lines. Note I'm reporting root-mean-squared error, not mean error, so positive and negative errors fail to cancel.
There's a bit of an error in the altitude in every case: around 174 cm. But the effect of the dynamic pressure is very small: just a few cm.
Were the effect larger, I could propose methods to try and correlate speed with altitude, and correct for that. But this error is so small, such an effort would likely do more harm than good. Indeed, on these data, when I tried to apply such a correction, the error increased: there's just not enough data in a typical ride to see such a small effect. So the conclusion is: don't worry about it.
Before that, I described how I'd combine a barometric altitude signal with a GPS signal to get the best of both: the short-term responsiveness and reliability of the barometric altimeter with the general accuracy of the GPS (at least when there's a signal). I'd applied this to randomly generated data, which were derived using a simple pacing model with the bike power-speed equations.
The effect of dynamic pressure on measured altitude is simply derived from Bernoulli's equation:
Δz = ‒½ ( kdp v )² / g,
where Δz is the error in altitude, v is the speed relative to the wind, kdp is the coefficient dependent on the altimeter position and orientation, and g is the acceleration of gravity.
The the smoothed average of the GPS signal is used to correct for errors in the barometric altimeter, how the dynamic pressure affects the derived altitude with my algorithm depends on how speed fluctuates, not just on the speed. So to account for this, I changed my assumption about power. Instead of a nice steady power, I assumed power fluctuates between 0% and 200% of the "optimal" value, varying sinusoidally with a period which I varied. Furthermore, just to be pedantic, for each period of power I used each of four phases. I did each of these "simulations" for kdp of 0 (no stagnation pressure effect) and 0.5.
Here's the result, where I only averaged over times starting with 100 seconds, to avoid the details of the initial acceleration having too much effect:

The dotted lines show the result with the smooth power. The oscillating power results are shown by the dots connected by the lines. Note I'm reporting root-mean-squared error, not mean error, so positive and negative errors fail to cancel.
There's a bit of an error in the altitude in every case: around 174 cm. But the effect of the dynamic pressure is very small: just a few cm.
Were the effect larger, I could propose methods to try and correlate speed with altitude, and correct for that. But this error is so small, such an effort would likely do more harm than good. Indeed, on these data, when I tried to apply such a correction, the error increased: there's just not enough data in a typical ride to see such a small effect. So the conclusion is: don't worry about it.

Comments