combining GPS and barometric altimetry: correcting the barometric data
Okay, back to altimetry.
After painstakingly constructing simulated altitude data consisting of the following:
So the approach I take is to first identify points at which the GPS signal is good. At those points, I calculate a difference between the GPS and barometic altitudes. I then locally average these distances using my favorite smoothing function, cosine squared:
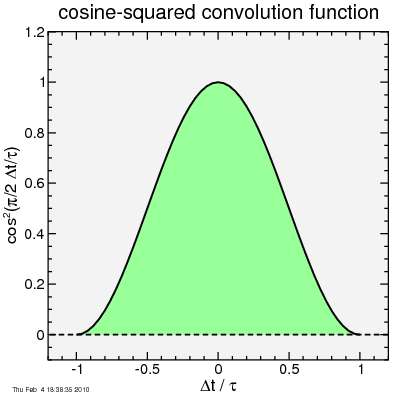
The key is to pick the time constant. Too short a time constant, and you don't suppress the GPS fluctuations. Too long a time constant and the barometric error may change sufficiently that the correction is no longer accurate. So I picked:
τ = 100 seconds.
When the GPS signal drops out, I don't do the averaging to calculate the correction amplitude: I instead linearly interpolate between the correction altitude of the nearest points before and after the point without the GPS signal. Remember I'm doing this analysis at the end of the ride, so I have access to all of the data, not just the points preceding the point I'm presently analyzing.
Of course, if there's no GPS at the beginning of the ride, for those points I need to simply use the next available calculated offset. At the end of the ride, if there's no GPS, I use the last calculated offset.
Simple. So here's the result applied to my test data, again showing the second hour of the "ride" (the most interesting part):
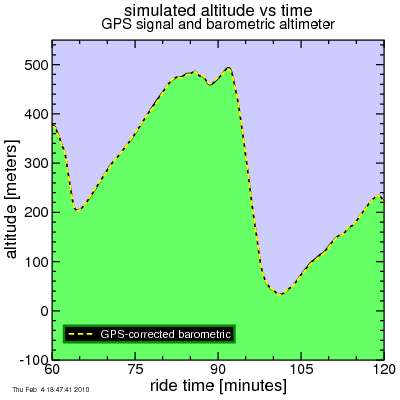
It's easy to see the corrected barometric altitude tracks the true altitude very nicely.
Let's look a bit closer: here's a histogram of the errors of the GPS altitude and the corrected barometric altitude, using the entire ride (ten thousand seconds). The error in the uncorrected altitude is too large to fit on the plot, so is omitted:
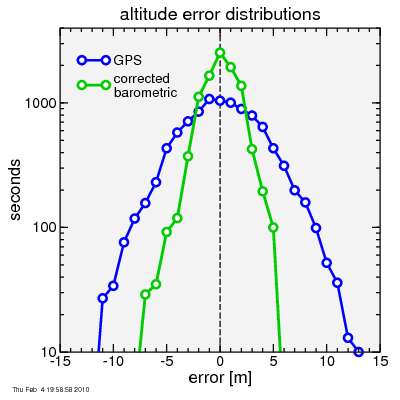
In addition to the corrected barometric altitude being much smoother than the GPS altitude, the errors at any given time point also tend to be smaller.
The smoothness is examined by doing a Fourier transform of the error. The following shows the result for the barometic altimeter, the GPS altimeter, and the corrected barometric altitude data:
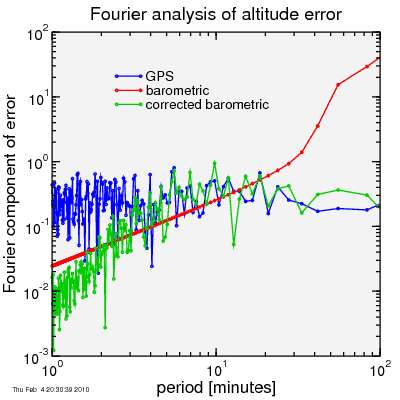
The short-term variation in the corrected barometic altitude (to the left of the plot) is much lower. The barometic altimeter as enormous long-term swings in its error, but the corrected barometic altitude is immune from these, since it is held in line by the GPS signal. Yet it is relatively free of the GPS signal's short-period errors. Long-term, it tracks the GPS accuracy.
So there it is. My scheme worked nicely. At least in simulation, that is. It would be fun to try it on actual data. Of course with actual data one doesn't have a "true" altitude. The best one can do is to ride the same road repeatedly, and look for consistency in the result.
An intriguing idea was presented to a previous post in comments: that the barometic signal would be subject to short-term errors from air speed changes as the bike speed varies. I'll look at that in a future post, and show how I might deal with that issue.
After painstakingly constructing simulated altitude data consisting of the following:
- true altitude
- GPS altitude signal: tends to fluctuate and drop out for periods, never deviates too far from the true altitude, at least in my model
- barometric altitude: smoother than the GPS and never drops out, but has a slowly varying offset from the true altitude
So the approach I take is to first identify points at which the GPS signal is good. At those points, I calculate a difference between the GPS and barometic altitudes. I then locally average these distances using my favorite smoothing function, cosine squared:

The key is to pick the time constant. Too short a time constant, and you don't suppress the GPS fluctuations. Too long a time constant and the barometric error may change sufficiently that the correction is no longer accurate. So I picked:
τ = 100 seconds.
When the GPS signal drops out, I don't do the averaging to calculate the correction amplitude: I instead linearly interpolate between the correction altitude of the nearest points before and after the point without the GPS signal. Remember I'm doing this analysis at the end of the ride, so I have access to all of the data, not just the points preceding the point I'm presently analyzing.
Of course, if there's no GPS at the beginning of the ride, for those points I need to simply use the next available calculated offset. At the end of the ride, if there's no GPS, I use the last calculated offset.
Simple. So here's the result applied to my test data, again showing the second hour of the "ride" (the most interesting part):

It's easy to see the corrected barometric altitude tracks the true altitude very nicely.
Let's look a bit closer: here's a histogram of the errors of the GPS altitude and the corrected barometric altitude, using the entire ride (ten thousand seconds). The error in the uncorrected altitude is too large to fit on the plot, so is omitted:

In addition to the corrected barometric altitude being much smoother than the GPS altitude, the errors at any given time point also tend to be smaller.
The smoothness is examined by doing a Fourier transform of the error. The following shows the result for the barometic altimeter, the GPS altimeter, and the corrected barometric altitude data:

The short-term variation in the corrected barometic altitude (to the left of the plot) is much lower. The barometic altimeter as enormous long-term swings in its error, but the corrected barometic altitude is immune from these, since it is held in line by the GPS signal. Yet it is relatively free of the GPS signal's short-period errors. Long-term, it tracks the GPS accuracy.
So there it is. My scheme worked nicely. At least in simulation, that is. It would be fun to try it on actual data. Of course with actual data one doesn't have a "true" altitude. The best one can do is to ride the same road repeatedly, and look for consistency in the result.
An intriguing idea was presented to a previous post in comments: that the barometic signal would be subject to short-term errors from air speed changes as the bike speed varies. I'll look at that in a future post, and show how I might deal with that issue.

Comments
Where the two overlap, even better.
Anyway, I happened on this page when I realized my new phone has GPS, pressure, and even acceleration and gyroscopic sensors. There must be a good app that will turn that data into good altitude data. Okay, probably not the force sensors, intagrating them would probably kill the battery.
Haven't found that app yet...
Thanks for your interesting posts.
-kb
kentborg you-know,at borg.org
http://borg.org