Bernoulli, stagnation pressure, and barometric altimeters
I never could wrap my head around this stuff.
Bernoulli's_principle basically says that when an incompressible fluid is moving more rapidly, the pressure drops. Air is obviously included in the list of incompressible fluids, leading to all the activity at SFO not so far south of where I live.
In some physics class in my distant pass, the professor justified this by launching into a set of differential equations. You stare at the equations, one after another, and sure enough it's hard to dispute any one of the steps, but that doesn't mean the result actually makes any sense. Differential equations, after all, are just a model. There's no physics in differential equations. The physics is in particles bouncing around: scattering elastically and inelastically, transferring momentum, transferring energy. Scattering, if anything, is the heart of physics.
So I envision gas molecules bouncing around, energy scattering between various degrees of freedom, minding their own business. Along comes a cyclist with his altimeter, a pressure sensor, mounted horizontally on the bars. Gas molecules now start bouncing off the pressure sensor, and these collisions transfer momentum, which implies a force, which implies a pressure. So the sensor measures a pressure. Higher altitude means fewer air molecules means fewer collisions means lower pressure. So the pressure gives me a hint to what the altitude is. The question is: how is the measured pressure affected by the bike's motion through the air?
First consider an idealized case, with the sensor mounted perpendicular to the direction of motion of the bike through the air. Does the pressure against the spring change when the bike is moving?
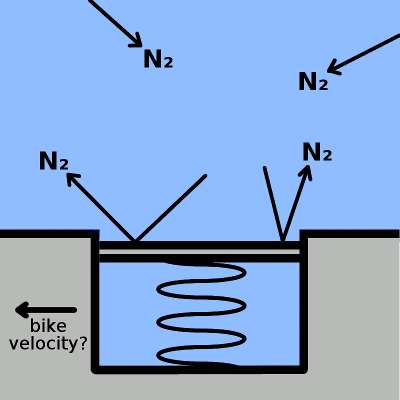 Simple man's view of a pressure sensor: a spring compresses due to gas molecule impacts. Does the compression reduce if the platform is moving sideways? From this diagram, there's no reason to believe it should. Gas particles have the same kinetic energy in the vertical axis whether or not the sensor is moving, it seems.
Simple man's view of a pressure sensor: a spring compresses due to gas molecule impacts. Does the compression reduce if the platform is moving sideways? From this diagram, there's no reason to believe it should. Gas particles have the same kinetic energy in the vertical axis whether or not the sensor is moving, it seems.
Particles bounce off the sensor surface with a particular kinetic energy component perpendicular to the sensor surface. How does this kinetic energy component care if the platform is moving laterally or not? It seems like the pressure associated with these collisions should be independent of lateral motion of the sensor. Really, they don't.
A common view of Bernoulli is "faster moving particles, at a given number density and temperature, exert a lower pressure in all directions." Bzzzt. This can't possibly be right.
The question here: does Bernoulli's Principle imply that the gas pressure will be reduced at the pressure sensor when the bike is moving? According to Wikipedia, the Bernoulli Principle is a statement that total pressure is constant everywhere in the fluid flow, where total pressure includes both the static pressure and the dynamic pressure. It is a statement of conservation of energy: that if gas is moving in a non-random direction, then the kinetic energy remaining for random motion is less.
But nothing about it says total energy is independent of the frame of reference. In this case, changing the frame of reference from one stationary in the gas to one moving through the gas increases the kinetic energy per gas molecule (kinetic energy depends on the frame of reference). It increases equal to the value predicted by the "dynamic pressure: ½ M v², where v is the bike speed and M is the mass of a gas molecule. So the conclusion in this case is the pressure reading will not change as long as the pressure meter is located perpendicular to the direction of motion.
To check this, let's whip out the Navier-Stokes equation, which I'd earlier said the professor had written on the board in class:
ρ ( ∂v/∂t + v·∇v ) = ‒∇p + ∇×T + f,
where ρ is the mass density, v is the fluid velocity vector, p is the pressure, T is the stress tensor, and f is the force on the fluid. Basic Newton's laws combined with mass continuity. Nothing obscure.
And it basically agrees. Pressure changes come from velocity which changes over time (∂v/∂t) or over space (∇v). If the velocity is uniform and constant, and you're not pushing on it or it's not falling, no problem. If it's changing over time because the velocity of the reference frame has a time-dependent velocity (the pressure sensor is accelerating) then you're not using an inertial reference frame, and the equation no longer applies. Use an inertial reference frame.
So that's the case of the ideal horizontal mount. Now let's consider an alternate case: the pressure sensor is mounted horizontally, facing the wind:
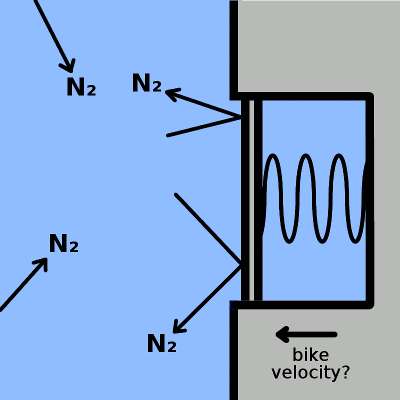 The same pressure sensor, this time facing the wind.
The same pressure sensor, this time facing the wind.
Now this is a different matter completely: it's easy to see how the wind pressure will affect the sensor. This is called the "stagnation pressure", and is exploited in the Pitot Tube, a speed sensor for sub-Mach airplanes.
But nothing is so simple. Any air sensor that's out in the wind is going to be exposed to wind deflected off the rider or by the bike, even if it's mounted horizontally. It's only a matter of how much. Which of course depends on how the sensor is packaged and mounted. Still, there could be an effect: most likely a positive correlation between speed and pressure (showing up as a negative correlation of calculated altitude). But the opposite correlation is also possible.
Next time I'll look at whether this is important, and if it is, how it might be addressed.
Bernoulli's_principle basically says that when an incompressible fluid is moving more rapidly, the pressure drops. Air is obviously included in the list of incompressible fluids, leading to all the activity at SFO not so far south of where I live.
In some physics class in my distant pass, the professor justified this by launching into a set of differential equations. You stare at the equations, one after another, and sure enough it's hard to dispute any one of the steps, but that doesn't mean the result actually makes any sense. Differential equations, after all, are just a model. There's no physics in differential equations. The physics is in particles bouncing around: scattering elastically and inelastically, transferring momentum, transferring energy. Scattering, if anything, is the heart of physics.
So I envision gas molecules bouncing around, energy scattering between various degrees of freedom, minding their own business. Along comes a cyclist with his altimeter, a pressure sensor, mounted horizontally on the bars. Gas molecules now start bouncing off the pressure sensor, and these collisions transfer momentum, which implies a force, which implies a pressure. So the sensor measures a pressure. Higher altitude means fewer air molecules means fewer collisions means lower pressure. So the pressure gives me a hint to what the altitude is. The question is: how is the measured pressure affected by the bike's motion through the air?
First consider an idealized case, with the sensor mounted perpendicular to the direction of motion of the bike through the air. Does the pressure against the spring change when the bike is moving?
 Simple man's view of a pressure sensor: a spring compresses due to gas molecule impacts. Does the compression reduce if the platform is moving sideways? From this diagram, there's no reason to believe it should. Gas particles have the same kinetic energy in the vertical axis whether or not the sensor is moving, it seems.
Simple man's view of a pressure sensor: a spring compresses due to gas molecule impacts. Does the compression reduce if the platform is moving sideways? From this diagram, there's no reason to believe it should. Gas particles have the same kinetic energy in the vertical axis whether or not the sensor is moving, it seems.Particles bounce off the sensor surface with a particular kinetic energy component perpendicular to the sensor surface. How does this kinetic energy component care if the platform is moving laterally or not? It seems like the pressure associated with these collisions should be independent of lateral motion of the sensor. Really, they don't.
A common view of Bernoulli is "faster moving particles, at a given number density and temperature, exert a lower pressure in all directions." Bzzzt. This can't possibly be right.
The question here: does Bernoulli's Principle imply that the gas pressure will be reduced at the pressure sensor when the bike is moving? According to Wikipedia, the Bernoulli Principle is a statement that total pressure is constant everywhere in the fluid flow, where total pressure includes both the static pressure and the dynamic pressure. It is a statement of conservation of energy: that if gas is moving in a non-random direction, then the kinetic energy remaining for random motion is less.
But nothing about it says total energy is independent of the frame of reference. In this case, changing the frame of reference from one stationary in the gas to one moving through the gas increases the kinetic energy per gas molecule (kinetic energy depends on the frame of reference). It increases equal to the value predicted by the "dynamic pressure: ½ M v², where v is the bike speed and M is the mass of a gas molecule. So the conclusion in this case is the pressure reading will not change as long as the pressure meter is located perpendicular to the direction of motion.
To check this, let's whip out the Navier-Stokes equation, which I'd earlier said the professor had written on the board in class:
ρ ( ∂v/∂t + v·∇v ) = ‒∇p + ∇×T + f,
where ρ is the mass density, v is the fluid velocity vector, p is the pressure, T is the stress tensor, and f is the force on the fluid. Basic Newton's laws combined with mass continuity. Nothing obscure.
And it basically agrees. Pressure changes come from velocity which changes over time (∂v/∂t) or over space (∇v). If the velocity is uniform and constant, and you're not pushing on it or it's not falling, no problem. If it's changing over time because the velocity of the reference frame has a time-dependent velocity (the pressure sensor is accelerating) then you're not using an inertial reference frame, and the equation no longer applies. Use an inertial reference frame.
So that's the case of the ideal horizontal mount. Now let's consider an alternate case: the pressure sensor is mounted horizontally, facing the wind:
 The same pressure sensor, this time facing the wind.
The same pressure sensor, this time facing the wind.Now this is a different matter completely: it's easy to see how the wind pressure will affect the sensor. This is called the "stagnation pressure", and is exploited in the Pitot Tube, a speed sensor for sub-Mach airplanes.
But nothing is so simple. Any air sensor that's out in the wind is going to be exposed to wind deflected off the rider or by the bike, even if it's mounted horizontally. It's only a matter of how much. Which of course depends on how the sensor is packaged and mounted. Still, there could be an effect: most likely a positive correlation between speed and pressure (showing up as a negative correlation of calculated altitude). But the opposite correlation is also possible.
Next time I'll look at whether this is important, and if it is, how it might be addressed.

Comments
Oh...and I saw your post over on BTR. I think the "mistake" is your assumption of the speed when the max delta elevation was seen...it was more like 15 m/s, or ~54 km/hr at those points.
Good point on the stagnation bubble! That makes sense. Although then the question arises to what a theoretical value for the velocity (or dynamic pressure) multiplier is (the pressure multiplier the square of the velocity multiplier). With your "bubble" concept, it stands to reason this number might be fairly large.
Also, I'm not sure about your equation for "delta z"...I used the equation that the stagnation pressure(in Pascals) was = 1/2*rho*(alpha*V)^2. I then converted the stagnation pressure to equivalent elevation difference, which is basically linear at low elevations (IIRC it was 1 millibar per 8 meters...but I'm having a hard time recreating the altitude conversion factor I used in the spreadsheet) Make sense?
Think about it this way: the pressure at a given altitude = the weight of all air in a column above that altitude. So if I change altitude by Δz, the change in pressure is the change in weight of the column. That's the negative of the weight-density of the air multiplied by the height difference, where weight = gravity multiplied by mass, so if I know the mass density ρ (mass per unit volume = mass of a gas molecular multiplied by molecules per unit volume), I multiply by g and Δz and take the negative, and that gives me the change in pressure with height. That's how the altimeter measures height (for ρ, it uses the ideal gas law, so it needs T, also).
So then I consider the dynamic pressure. That's just from Newton's law: pressure = kinetic energy of the scattered air per unit are = ½ ρ v².
So if I then calculate the equivalent altitude change from this "dynamic" pressure, I the ρ cancels. I get:
Δz = ½ v² / g
Very simple. No rules of thumb for pressure change with altitude required.
I think the confusion came into this from my terminology about what % of free stream velocity was "presented" to the sensor. You were looking at it as what amount was actually being stopped at the sensor, while I was referring to how much was flowing past the sensor (i.e. the % of free stream was what had NOT been stopped by the "bluff body").