hacking

I'm a bit better than I was yesterday, but still generally out of commission. I drowned my personal sorrows in my sorry physical state by hacking GoldenCheetah, a great project for managing power meter data. GoldenCheetah has been around for several years, but thanks to a recent infusion of excellent contributions from Ned Harding, it's finally become for me a useful tool.

I decided to dive in and try to implement a critical power model extraction technique I've been thinking about. The critical power model says a rider can produce a given level of "aerobic" power (the "critical power", or CP) forever, but additionally has a fixed budged of "anaerobic work" capacity (AWC) which can be spent as extra power. The shorter the total effort during which the anaerobic work is spent, the higher the average power during that period. For such a simple model, it seems to work fairly well.

Power-based training isn't typically based on the critical power, but rather on a "threshold" power which is less sustainable. Andrew Coggan, in his excellent book (written with Hunter Allen) Training and Racing with a Power Meter, advocates the definition of a "functional threshold power" equal to the maximum power a rider can sustain for an hour. Basically start fresh, perfectly dial in your sustainable power, and collapse in an exhausted heap at the end of the hour. Hard to do, obviously.

Since it's so hard to nail the perfect one-hour effort, typically FTP is extracted using shorter efforts. For example, power averaged during a 20 minute effort might be discounted 5% to estimate FTP. But the problem remains: you've got to nail that 20 minute effort. And even if you do, not everyone can sustain the same fraction of power when increasing an effort from 20 minutes to the full hour. For example, Eric Heiden had the record (14:15) up Old La Honda Road, despite the fact that even a quick glance at Eric's legs show he's not a spindly climber-type. Yet he was able to excel at the (by Euro standards) short 390 vertical meters of Old La Honda, whereas he wouldn't rank as high on a climb four times that length. You see this in European racing, where guys like Samuel Sanchez who might break away over the relatively short climbs in Liege-Bastogne-Liege can't always hang with the best up L'Alpe d'Huez or Mont Ventoux.

So I prefer rolling out the critical power model for this purpose. Instead of using a single 20 minute effort, combine two different efforts using the two power values to estimate the two parameters of the critical power model: CP (measured in watts) and AWC/CP, the latter the time during which the model predicts one could ride at double CP (in reality the model breaks down at short efforts, so this may not be attainable). This shorter effort should be long enough that one can fully "spend" AWC, but short enough that AWC is responsible for a considerable fraction of total power, improving the sensitivity of that parameter estimate.

But the rider still needs to do two essentially perfect efforts at these two time intervals. In reality, we often ride hard for various distances or times, but we don't always know ahead of time how long we'll be able to sustain a given level of power. Given a large body of data, wouldn't it be better for an algorithm to figure out from the data itself which interval lengths work best for estimating the CP model parameters?

The scheme I came up with is the following:

1. Make an initial guess for AWC/CP.
   
2. For time intervals from 12 to 60 minutes, calculate the value of CP necessary to match the maximum power the rider was able to sustain for each time period.
   
3. Choose the maximum of these CP values as the estimate of CP.
   
4. Now forget about the previous value of AWC/CP. For each time interval from 2 minutes to 6 minutes, calculate the value of AWC/CP which would be needed to match the maximum average power sustained over the interval given the current estimate of CP.
   
5. Choose the largest of these values as the estimate of AWC/CP, unless the number is less than 30 seconds, in which case use that. The reason for this lower bound is because it's quite possible a set of data lacked anaerobic efforts of sufficient quality. For example, during base training, or during races where there was never the luxury of an absolutely maximal 2-6 minute effort starting fresh.
   
6. If the value of AWC/CP changed by more than some threshold (for example 1 milliminute), then use this new value and go back to re-estimate CP.
   
7. Then, given AWC and CP, FTP is simply calculated: FTP = CP + AWC / 1 hour.
   

Once I got over my fear of C++ (I'm basically a Perl hacker) and QWT, relying on the nice examples packaged with the QWT source code, I found it wasn't as hard as I'd feared to implement my algorithm. Here's a result (click on the image for a larger version).


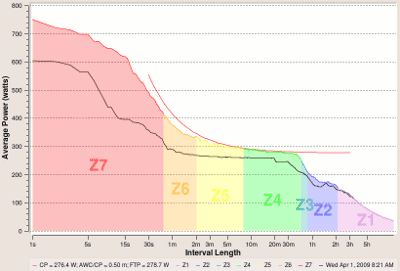
CP model and derived zones with March maximal power curve as displayed by my hacked version of GoldenCheetah
It's a bit busy... first, the black line shows the maximal power curve for a given ride. In the rainbow colors is plotted the maximal power curve derived from all rides in the data set (in this case, March-to-early April rides). The smooth red curve is the critical power model derived to fit these data. That smooth curve is used to estimate the power I could have sustained for an hour, my estimated FTP, and that FTP was used (with Coggan's recommended conversion factors) to generate my seven power-based training zones. These training zones were used to color-code the maximal power curve.

It came out looking better than I anticipated, I must admit. Hopefully some version of this can be incorporated into the official GoldenCheetah release at some point. There's still work to be done.