cross-chaining on SRAM 1×11
There's been an almost religious response to SRAM releasing 1×11 for the road. I find this puzzling, as to me it represents a valid choice for riding where super-wide range gearing isn't needed. And in the vast majority of the United States, the idea regularly riding extended steep climbs is at best a fantasy. It's restricted to European bike tours, etc.
1×11 provides basically the same gear spacing as 2×8, which honestly back in the day was fine, although also not for everyone, and those who wanted more went to triple chainrings. Today a lot of those who used triples back then are fine with wide-range 2×10 and 2×11 options. But if you want to avoid dealing with a front shifter, and maybe save a bit of weight, 1×11 can be an attractive choice. I was riding with an old colleague from Stanford Cycling, Mark, who's been riding SRAM 1×11 on hilly San Francisco Bay area rides and he loves it. But then he started racing with 2×6, and so learned to ride at a somewhat wider cadence range than riders starting today seem to require.
But one good argument against 1×11 is cross-chaining. We were all taught to not cross-chain. Riding in the big-big or small-small combination causes a lot of friction, it's always been said, and indeed when you spin your chainring backwards in a big-big combo there's a lot more resistance than when it's in a gear with less lateral chain deflection. But when applying power, how much difference is there?
My favorite source on such matters is FrictionFacts, and they did a study on drivetrain losses in various gears. It's reported by Bike Radar.
Here's a key plot from the report. It shows drivetrain losses in various gears on a 2×11 drivetrain:

In general, given the choice between two gear combinations at the same ratio, you take the big-big combination versus small-small. This is because the big-big combination will have the chain under lower tension and the chain will bend less each time it moves off the rear cog and when it moves onto the front chainring. The chain also bends on the pulleys and on the bottom of the chain run, but down there it's under lower tension. So what matters most is when it's under high tension, on the top.
But the big-big combinations tend to have inferior chainlines at the low end of the gear range. You can see it in the plot. Not this isn't an ultra-dramatic effect, and I used to vastly underestimate it based on backward-spinning experiments. The big-big combination is less than a watt higher than the alternative at the same ratio with the small ring. But still, I'll save a watt if I can.
With a 1×11 system the chainring sits aligned with the 6th cog in the back, counting the cogs 1-11. That's 5 cogs to the right, 5 cogs to the left, one perfectly aligned. With a 2-11 system, given my measurement of 9 mm of separation between the small and large chainrings, which is 2.4 cog spacings, that puts the chainrings in positions 4.8 and 6.2. If you always optimized your front chainring choice based on chain line it seems 2×11 should provide on average a better chainline than 1×11, by virtue providing more choice. And indeed if we ran, for example, a 44-44 front, that would obviously be true. I could pick my front ring based only on chain line.
But we don't run 44-44. Instead we pick the front ring based on whether we want a higher or lower gear range. Typically front shifts are a relatively last resort, if the present ring choice is running up against one or the other limit. So in real life, what gears to riders pick?
Now I don't claim to have nearly enough data to study this in depth. But I do have sample data from DC Rainmaker, who was testing the Garmin Edge series support for Di2 reporting via ANT+ Sport of gear choice. Here's a table from DC Rainmaker:
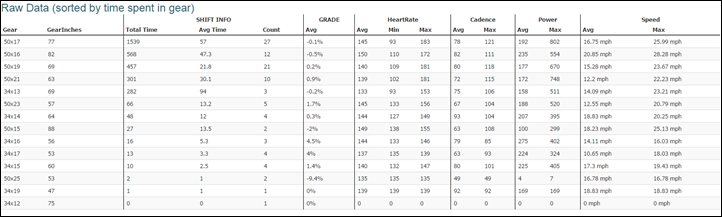
What I did here was to calculate the front chainring position (4.8 or 7.2) versus the rear cog position (1 to 11) and calculated from that the chain deflection in cog spacing equivalents. Weighting these by time spent in each gear I was able to calculate an average chain deflection of 2.6 cog spacings for this ride. I determined that he could have done the same ride with a 44 tooth chainring in the front using 1×11 with the same 11-25 range in the back. So I then repeated the calculation using the closest gear in that 1×11 system, assuming the front chainring as in position 6. Surprise, surprise, surprise: the average chain deflection was now 1.4.

How is this possible? The reason is that DC Rainmaker spent the vast majority of the ride in the ratios which would have been provided by the middle 5 cogs with the choice of a 44 tooth chainring. These have deflections of -2, -1, 0, 1, and 2. A time-weighted average of the absolute value of the chain deflection thus yields the remarkably small number of 1.4.
I'm sure if I were to look at another ride, for example one with super-steep climbs and extended fast descents where the rider spent a large fraction of the time at the absolute extremes of available gears, the chain line result would have been different. But for relatively flat rides the 1×11 system may actually provide superior chain lines, based on this N=1 example.
But keep in mind on all of this we're dealing with a fraction of a watt in drivetrain losses. I like obsessing over this sort of thing but if you're just going out for a training ride it's essentially irrelevant. You're better off worrying about keeping your zipper shut and wearing tight-fitting rather than loose-fitting clothing.

Comments
That said, since losses aren't necessarily proportional to deflection across the entire range, I'm not sure how indicative of "good or bad" the average deflection metric is.
But I'm using a "real world" example of a rider who isn't thinking much about chainline when he's riding other than to avoid extreme cross-chaining. Sure -- this is a ride probably near Paris, where it's mostly flat, but then a lot of riders do the vast majority of their riding on such terrain (New York, Chicago, Philadelphia, DC, Boston, ... most major US cities). And the result is the chainline can actually be better.