attempt at calculating effect of random-direction wind
Last time, I discussed a simple approximation which comes fairly close to predicting the speed at constant power in an arbitrary wind of reasonable magnitude. The formula can be written as a normalized speed s' (normalized to no wind) and a normalized wind sw' (normalized to the same scale) as follows:
where swx' is the normalized speed of the wind in the direction of the rider (positive for tailwind, negative for headwind).
For a typical closed circuit, the rider will head in random directions relative to the wind. If the wind is constant than the average distance-weighted direction is zero: the rider starts where he begins. Last time I calculated a result assuming a square course aligned with the wind. That's an over-simplification, even if it's probably representative. But I'd prefer to consider the more generally applicable case of all directions equally likely.
So I assume the rider goes in a big circle. I can then integrate 1/s' around the circle. 1/s' is the time taken per unit distance for a given point on the course. The equation as follows:
where the integral goes from 0 to 2π.
Note that swx' is a function of φ so I need to convert one to the other to evaluate the integral. I want to avoid the exponential of a cosine (transcendental of transcendental) so I choose to get rid of φ:
I convert the differential dφ:
where I define a temporary variable:
I can get rid of the sin φ using:
The integral becomes:
where z goes from −1 to +1, and where I made a few trivial simplifications.
Here I'm stuck. It looks like it shouldn't be hard, but I simply don't know what to do next. It obviously converges despite going infinite at the endpoints of integration: for z = 1 - δ where δ is small and positive, 1 / sqrt(1 − z2) = 1 / sqrt(1 − (1 − δ)2) ≈ 1 / sqrt(1 − (1 − 2δ)) = 1 / sqrt(2δ), and the integral of that with respect to δ is sqrt(2δ), which goes to zero for δ from 0 to a small positive limit. So that's not a problem. But I was hoping for a simple analytic solution.
Back in the day, that would be the end of it unless I could come up with some clever approximation. But instead I quickly succumb to the temptation of numerical evaluation and fit so I can watch the cyclocross world championship web feed. The result is in the following plot:
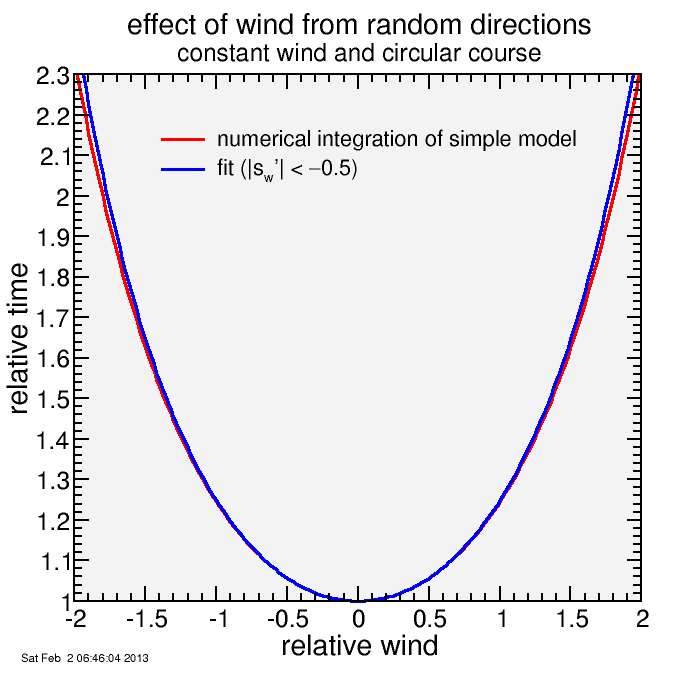
I did the fit using only the function from −0.5 to +0.5, since winds outside this range at ground level would be rare. Despite this, the function extrapolates nicely out to my plotted range of −2 to +2.
Converting from time to average speed, and going from normalized speeds back to actual speeds for rider and wind, the fit is:
Here's the same plot with log-log axes, showing the time delay rather than time:
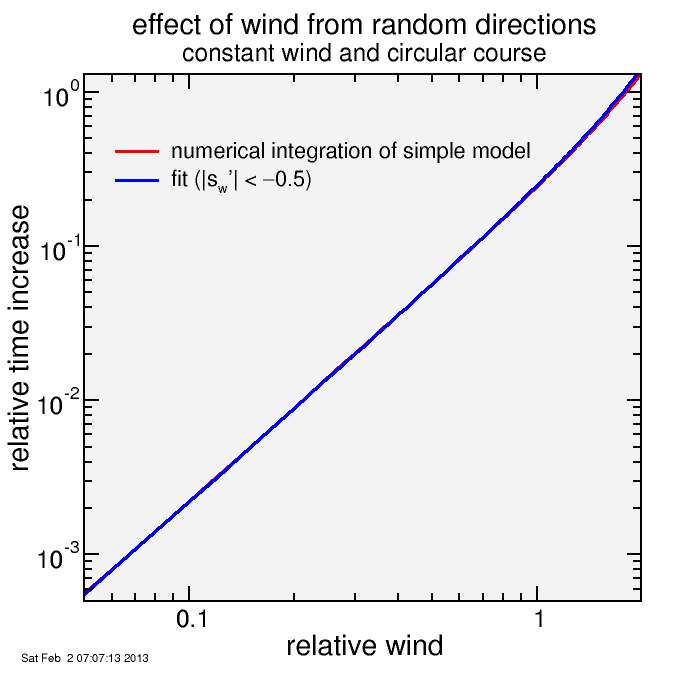
The result is a wind equal to half the zero-wind rider speed delays the rider around the circular course by approximately 5%.

Comments