Numerical Simulation of Low-Key 2012 week 4 Passing

Last time I made an off-the-cuff prediction each rider in today's Boulder Creek to Saratoga Gap Low-Key time trial would be passed, or be passed, by around 2 riders on average. That was based on the assumption riders varied by around 0.5% each in the sequence and that riders varied week-to-week by 2%. These were low estimates, I concluded, after examining the data.

For this post I actually did a numerical simulation, using numbers derived from Low-Key historical data.

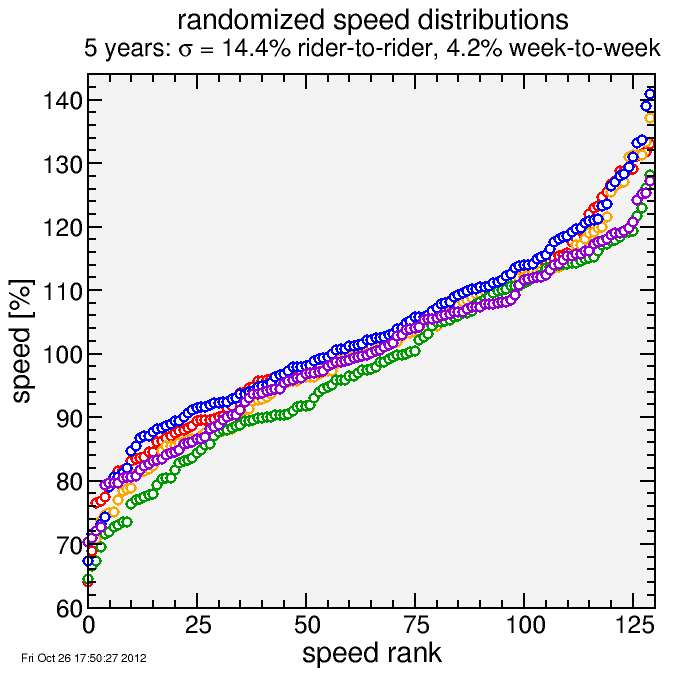
1. For each starter, I generated a normally distributed "true speed", with sigma = 14.4% about a mean (derived from historical data).
2. For each rider, I then ran a "qualifying climb" in which speed varied normally with sigma = 4.2% from true speed (derived from my score history). Note this was based on the old scoring system, % of median, which includes an artifact that some weeks tend to yield different amounts of score spread than others. So it's probably an over-estimate.
3. I assigned riders a start time based on the qualifying week, at one-minute intervals.
4. I again assumed speeds vary normally with sigma = 4.2% on the time trial climb, which for the average rider takes 1 hour.
5. I calculated the number of passes for each rider based on start order, and the number of times passed for the rider.
6. I did the experiment 100 thousand times, averaging the results.

On average each riders is passed, and passes, 2.29 times during the time trial. Riders starting first or last tend to be statistical outliers, and are passed, or pass more than this average. This result is around twice what I'd ball-parked last time, primarily because I basically doubled my estimate of week-to-week variability. The distribution of passes and being passed versus start position is as follows:

So the first rider off was passed an average of 20 times in around 90 minutes of riding. Of course, he/she doesn't pass anyone. The final rider passes on average around 3.5 riders, although the rider passing the most riders was the ninth, who passes approximately 6 riders. This is because the slower riders have more time to make up a one-minute gap than the fastest riders.

In 10 thousand separate repetitions, the extreme cases were 28 passes by a rider, and by some statistical fluke one rider was passed 104 times (different riders, different years). Unfortunately the model doesn't handle extreme outliers well: it allows for near-zero or even negative-speed riders if the random numbers come out that way. Even so, if this was the worst thing to happen in a 10 millenia of W Hwy 9, that wouldn't be so bad.

We'll see how it goes today...