Mount Diablo Time Trial: the numerator problem

Last post I talked about the denominator issue I had with the Diablo hillclimb time trial. There I converted my present weight to my weight when I set my Old La Honda PR late last year and concluded that my time, which would have put me 3rd in my category, was pretty good, and that therefore my numerator was fine: my power was basically on target.

But that level of analysis really doesn't stand muster. I have the data available to estimate my power: I just need to run the numbers.

I could use Strava's estimated power but that's based on an undocumented model. It's easy enough to download data from Strava myself and run my own calculations.

So here I go: Diablo starts at relatively low altitude and the time trial climbs a net of only 520 vertical meters so the air is fairly thick: I assumed 1.15 kg/m³. I know my mass at ride time (59 kg), my bike's mass (approx 5.1 kg), and the mass of stuff on my body (1.5 kg estimated). My tires are Vittoria Chronos pumped to 160 psi: good stuff. I estimate my rolling resistance coefficient at 0.3%. I don't know much about my wind resistance coefficient and area, but I'm tempted to use around 0.36 m². There might have been a bit of a tailwind, especially in the opening kilometers. I assume drivetrain losses are around 0.3%.

But before estimating power, it's good to try and validate the model against known data. I didn't have a power meter, but a friend, who I'll refer to as K, had a very nice Quarq crank-based unit. K claims to be 64 kg. I guessed his tires were slightly higher rolling resistance, so used 0.4% for his Crr. I assumed his bike weighs close to the UCI limit (which didn't apply at this race) so I used 7 kg for the bike mass. That might have been slightly high. That leaves CdA which is uncertain. He's taller than me and rail thin, which would imply a higher CdA, but he also had a skin suit while I had a standard jersey + bibs. I had tape on some of my helmet vents; I'm not sure about him. So overall I assume his CdA isn't that much larger than mine.

Unfortunately using a fixed CdA I couldn't get a good fit to his data unless I used a very low value and boosted his mass to unrealistic values. So instead I decided to use a two-phase CdA: a lower value for the flatter portion near the beginning,then a higher value for the climb proper. This made sense, both because I know I paid more attention to aerodynamics on the flat bit, then focused more on being relaxed on the steep climbing. I assume he did similar. Additionally, there might have been a more significant tail wind on the bottom portion. Tail wind can be modeled directly, but I decided to just fold that into an effective CdA reduction, since I wanted to reduce the number of knobs to turn.

So I modeled CdA with an error function, starting at 0.26 for K then increasing to 0.36 m². For me, I then assumed a similar pattern, but reduced the values by 0.01 m² for reasons I described.

Here's K's data along with the power I calculated, each smoothed with a 15-second time constant. He rode an excellent time trial, with data virtually constant throughout at 5.04 W/kg. And it paid off for him with a win in his category.

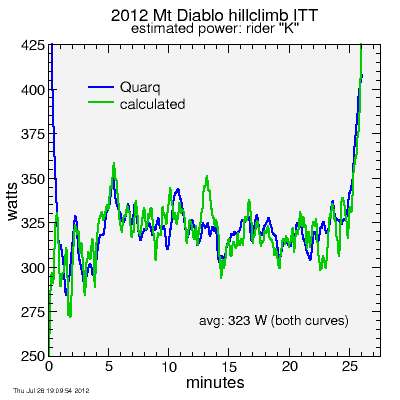
Calculated and measured power from rider K

Okay, now my turn. I felt fairly good about the model at this point so I applied it to myself. Here's what I get:

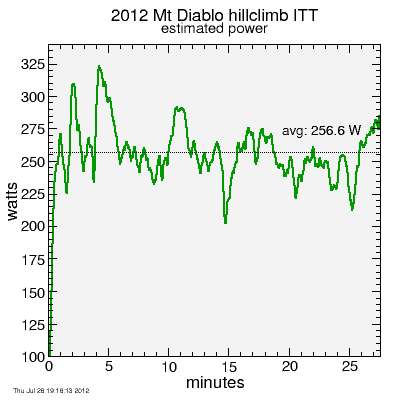
Calculated power from rider Me

My average power, according to this calculation, was 4.3 W/kg. Even were I a lean and mean 56 kg, what I was last winter, that would boost this only to 4.6 W/kg. That's well below my target 5 W/kg. On pacing, I clearly started harder than I was able to sustain going into the finish. But that's not, I would say, because I started too hard but rather because I finished too weakly. Of course, this depends on the assumption the power modeling I applied to rider "K" also applies to me. Wind conditions may have changed somewhat. But I'm going to stick with this analysis: I didn't feel as if I was going especially hard near the start.

There's a lot of assumptions in power modeling. For example, I could well be substantially off on the rolling resistance coefficient of my tires. But a more reliable calculation is to compare the results from Diablo to what an equivalent time would be up Old La Honda. Then if I underestimate rolling resistance up Diablo that gets to a large degree canceled by the reverse calculation underestimating the rolling resistance up Old La Honda.

Calculating instantaneous "Old La Honda" time needs to be done with a bit of care, because if power goes to zero, instantaneous OLH time goes infinite. So some smoothing needs to be applied to power before calculating time (you don't want to smooth time). Anyway, I applied 15 and 60 second smoothings to power before calculating "instantaneous" OLH time:

Instantaneous OLH time

In contrast, rider "K" was around 17 minutes.

So obviously I was not at my best at Diablo. Granted, I've done nothing to expect myself to be at my best: after hurting my back, I did virtually no training for a month in May-June, then came back doing a lot of volume without much intensity. But I don't like making excuses. Clearly both the numerator and the denominator weren't up to the task on Saturday.