Instant Runoff Election Simulation: Exhausted Ballots versus vote count in the 2011 San Francisco Mayor's race

The 8 November election in San Francisco will have 16 candidates contesting the mayor's position. The city will, for the first time, use instant runoff voting for the city-wide mayor's election, avoiding the need for people to cast multiple ballots in the likely scenario that no candidate would get at least 50% of the votes.

Instant runoff works by creating virtual "rounds" of voting. Voters get a number of votes on their ballot. They list their first choice, then their second, then their third for the mayor's position. In principle there could be enough votes to rank all candidates (one less than the number of candidates), or more if you want room for write-in candidates. First, all candidates receiving at least one first-place vote are ranked, and the one (or multiple) candidates receiving the least number of votes are eliminated (assuming there's at least one candidate left). Ballots which had an eliminated candidate as a first choice have lower-ranked choices promoted until either the first-place vote is still in the race or the ballot contains no more candidates within the race. A ballot with no more candidates who have not yet been eliminated is considered "exhausted". The election continues until a single candidate has a majority of the votes from unexhausted ballots.

People have argued that exhausted ballots are a sign of the failure of the system. They claim that voters who submit exhausted ballots haven't had their voice heard. Of course this is false: the voters have had their voice heard but the candidates they supported failed to garner enough support. However, what an exhausted ballot implies is that among the final candidates in the race, that voter failed to have his preference counted. Not counting write-in candidates, for a voter to be guaranteed that his ballot will not become exhausted, he needs a number of votes equal to the number of candidates minus one. This allows specification of a preference between every pair of candidates, covering the every possible final round.

But San Francisco doesn't provide this many votes: not even close. Due, it is claimed, to limitations of the ballots used in city elections, only three votes are offered. I view this as a bit of a farce: of course it is possible to provide space for more than three choices, and there are plenty of examples of other nations which do so. Three is a long, long way from the fifteen choices which would be necessary to avoid ballot exhaustion.

I'll assume voters pick their honest top choices, no matter the perception of candidate viability. Of course this is an incorrect assumption, voters may prefer their ballot not get exhausted early, and so may want to pick at least one candidate considered likely to get a large number of votes. This "safety net" pick would likely be in the final spot on the ballot, since picking it earlier would likely render "long-shot" choices ranking below the pick irrelevant. But I'll assume here that there's no safety net strategy, and voters pick their preference every choice. I also assume voters vote for the full number of slots on their ballot: if they have six choices, for example, they don't vote for three and leave the final three slots blank.

In this case, exhausted ballots only make a potential difference if the winner, after all other candidates but one have been eliminated, fails to receive at least half of the total ballots submitted (not half of the remaining unexhausted ballots). If the winning candidate receives over 50% of all ballots, then even if all exhausted ballots would have had their next vote go to the second-place candidate, that second-place candidate still would have received fewer votes than the winner. And that's an extreme case: it would be virtually impossible that every one of those voters with exhausted ballots would have preferred the loser over the winner. So unless the number of exhausted ballots is sufficiently larger than the difference in votes received in the final round by two surviving candidates, it is very unlikely those exhausted ballots would have switched the result if the voters had had more picks.

So how many exhausted ballots is acceptable? I'll toss out a proposal that 1% is okay, assuming there is a "cost" associated with putting more choices on the ballot. But more than 1% and I think it's fair to say the reduced number of votes per ballot is seriously in danger of affecting the outcome.

If I want to estimate how many votes I need per ballot, with 16 mayoral candidates, to avoid at least a 1% exhaustion rate I need to make further assumptions. With 16 candidates, if one candidate is vastly more popular than the rest, then he'll get most of the first-place votes, and no ballot will be exhausted, since the election end on the first virtual round.

In the other extreme, if each candidate is equally popular, such that a voter chosen at random will have ranked candidates in essentially a random order (assuming candidate preferences are uncorrelated, which is clearly unrealistic), then the fraction of ballots which will be exhausted can be calculated fairly easily: suppose there are C candidates and V votes per ballot. Then the number of ways to vote or the C candidates with V votes = C! / (C ‒ V)! ("!" is the "factorial" operator), while the number of ways to vote without including the final two candidates = (C ‒ 2)! / (C ‒ V ‒ 2)!, assuming C ‒ V > 1. Therefore the probability a random ballot will exhauste among many random ballots =

[ (C ‒ 2)! (C ‒ V)! ]/ [ C! (C ‒ V ‒ 2)! ].

This can be simplified to the following, eliminating the factorials:

(C ‒ V) (C ‒ V ‒ 1) / [ C (C ‒ 1) ]

But this case is unrealistic. Some candidates are more popular than others: the difference in votes isn't just due to randomness. So I'll make an assumption somewhere between the two cases of one super-popular candidate and all candidates equally popular. I'll assume the most popular candidate gets 20% of the first place votes. Then the second candidate gets 20% of the remaining votes. Then the third candidate gets 20% of the votes remaining after votes have been assigned to the first and second candidates. Etc. So the most popular candidate gets 20% of the first-place votes. The second-place candidate then gets 16% of the votes. Third place then gets 12.8% of the votes. This goes on to the least popular candidate, who gets 20% of the votes which haven't been assigned yet to that point, which is 0.7% of the total. If a voter has given his vote to none of the candidates after this round (2.8% of them), I try again starting with the most popular candidate. For second-preference votes and beyond, I do the same game, except a voter can only vote or each candidate once. So less popular candidates have a better chance of getting lower-ranked votes than they have of getting first-place votes.

This vote distristribution is simplistic, obviously. In a real election there will be pairs of candidates who will be close to each other: the gaps between canddidates won't be so uniform as they are in this model. But that's not so important. What's important is that the votes tend to be clumped toward the head of the field, rather than distributed uniformly over all candidates.

So I ran 100 thousand randomized votes using this approach, and I compared it to the "worst-case" where each of the 16 candidates is equally popular. Here's a plot of the percentage of exhausted votes versus the number of votes per ballot.

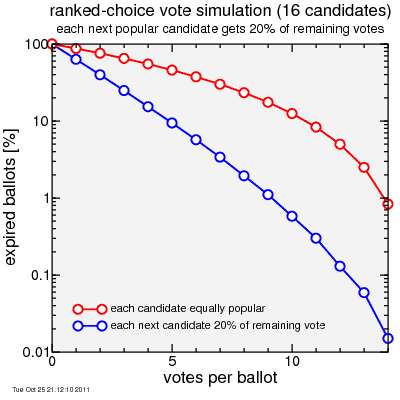
The result is for the equally popular candidates you need 14 votes per ballot to keep the exhaustion rate down to 1%. This is only one away from the 15 needed to fully rank the 16 candidates. For the candidates with different popularity, you need 9 votes to get the exhaustion rate down to close to 1%. In each case allowing only 3 votes per ballot will result in high exhaustion rates: 65% and 25%. With only 3 votes per ballot, the number of votes is affecting the outcome: either a lot of ballots get exhausted or voters, to avoid ballot exhaustion, will deviate from their true preferences by engaging in the self-fulfilling prophecy of voting for whom they think are "viable" candidates.

And since everyone agrees interim Mayor Ed Lee is a viable candidate, I don't like where this leads.

So in summary: I really like ranked choice voting, but surely we can do better than this. With 16 candidates, I want at least 9 slots to rank candidates, and would prefer 15, but would even live with as small a number as 6. 3 is obviously way too few, however.