Rating Climbs: Bohlman-Norton-Kittridge-Quickert-On Orbit-Bohlman
Here's some simple examples of running the proposed formula, which is:
rating = net climbing × (1 + [ 10 × net climbing / distance ]²)
Here's the profile for a climb which was used in the Low-Key Hillclimbs in 2009, Bohlman-Norton-Kittridge-Quickert-On Orbit-Bohlman (for brevity, I'll refer to this as "Bohlman-Norton" from here on):

The obvious question on this route is: is it one climb or two? John Summerson ends the main "climb" at the top of On Orbit Lane, right before the short descent at near mile 2.5, with what follows after corresponding to a second "climb".
For each possible segment length, I then found the segment which maximized the net climbing. This maximizes the rating. The top of On Orbit is often the optimal point to finish the "climb", until the segment length becomes so long that the subsequent descent must be included. It actually turns out to be more beneficial to start the climb at the beginning of the steep section near 1.5 km than to finish it at On Orbit, for some segment lengths. Note for simplicity in calculation I've switched to metric units instead of the imperial units usually used in the Low-Key Hillclimbs:

I then calculated the rating associated with each of these segments
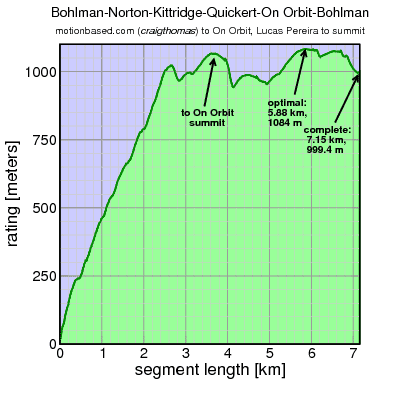
The x-axis shows the length of the road segment used for calculating the rating, while the y-axis shows the rating which results from that segment. Initially, the longer the climb, the more climbing, all of it the relatively steep section up to 4 km (2.5 miles), and the rating increases. But then then the algorithm is forced to accept the descent from On Orbit, dropping the rating. Adding more distance, it includes the climbing beyond On Orbit, and the rating increases again, eventually passing the previous peak which ended at On Orbit summit. Longer than this global optimum and the final rollers at the finish force the rating down again.
Here's the profile again, plotted in metric instead of imperial units, with the segment yielding the optimum rating shaded green. It begins 160 meters after the start of the Low-Key Hillclimb, and ends at On Orbit summit at 4 km.

So what's the conclusion? Basically that it's a better climb including the On Orbit descent and the climbing which follows than it is to end at the On Orbit summit, at least according to the rating scheme. I say "better" instead of "harder" because of course adding distance and climbing is going to make it tougher, but the purpose of the rating is to rate the climb itself, a subtle distinction.
Next I'll look at statistics from a broader set of climbs.
rating = net climbing × (1 + [ 10 × net climbing / distance ]²)
Here's the profile for a climb which was used in the Low-Key Hillclimbs in 2009, Bohlman-Norton-Kittridge-Quickert-On Orbit-Bohlman (for brevity, I'll refer to this as "Bohlman-Norton" from here on):

The obvious question on this route is: is it one climb or two? John Summerson ends the main "climb" at the top of On Orbit Lane, right before the short descent at near mile 2.5, with what follows after corresponding to a second "climb".
For each possible segment length, I then found the segment which maximized the net climbing. This maximizes the rating. The top of On Orbit is often the optimal point to finish the "climb", until the segment length becomes so long that the subsequent descent must be included. It actually turns out to be more beneficial to start the climb at the beginning of the steep section near 1.5 km than to finish it at On Orbit, for some segment lengths. Note for simplicity in calculation I've switched to metric units instead of the imperial units usually used in the Low-Key Hillclimbs:

I then calculated the rating associated with each of these segments

The x-axis shows the length of the road segment used for calculating the rating, while the y-axis shows the rating which results from that segment. Initially, the longer the climb, the more climbing, all of it the relatively steep section up to 4 km (2.5 miles), and the rating increases. But then then the algorithm is forced to accept the descent from On Orbit, dropping the rating. Adding more distance, it includes the climbing beyond On Orbit, and the rating increases again, eventually passing the previous peak which ended at On Orbit summit. Longer than this global optimum and the final rollers at the finish force the rating down again.
Here's the profile again, plotted in metric instead of imperial units, with the segment yielding the optimum rating shaded green. It begins 160 meters after the start of the Low-Key Hillclimb, and ends at On Orbit summit at 4 km.

So what's the conclusion? Basically that it's a better climb including the On Orbit descent and the climbing which follows than it is to end at the On Orbit summit, at least according to the rating scheme. I say "better" instead of "harder" because of course adding distance and climbing is going to make it tougher, but the purpose of the rating is to rate the climb itself, a subtle distinction.
Next I'll look at statistics from a broader set of climbs.

Comments