Powertap Torque Test: Post-Service
Saris sent me back my powertap wheel after I'd sent it to them for torque-tube test. Hats off to Saris: they did it w/o charge and returned it to me quickly. But had they actually done anything?
Unfortunately I didn't follow up their quick return with a quick re-test. Honestly, I found it liberating to not have power numbers telling me how lame I was every single ride. It was fun to just ride. I didn't need the power meter to tell me if I was going hard or not.
But eventually I couldn't ignore it any longer. So time for the torque test, again.
My procedure was slightly modified, after what I'd seen a friend do with his. To optimize the crank orientation (the weight needs to hang perpendicular to the crank or the torque estimate will be off), I grabbed the rear wheel and rotated in, forward and backward, until I saw the Powertap torque reach a maximum value. But here I deviated from my friend's approach: instead of using this number, I grabbed the brakes, let things settle out, then used that number. So my data taken here, like data previously, were done with the brakes holding the wheel. My reasoning was I wanted to make sure the wheel was stationary, and the brakes could do this better than my hand holding the rear rim.
Okay, cut to the chase:
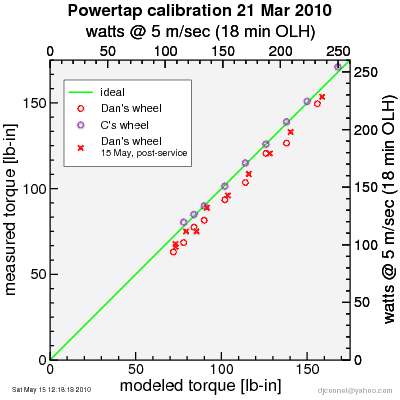 Retested powertap, compared with previous test of my wheel and a reference ("C") wheel.
Retested powertap, compared with previous test of my wheel and a reference ("C") wheel.
So it appears as if nothing has changed.
To test whether either wheel significantly deviates from the optimal curve, I did a t-test:
result is generally consistent with random variation combined with the
actual value being zero.
So on the reference wheel, the t-value for both the offset and the deviation of slope from 1 have low t-values. This is what I'd expect, assuming all torque is transferred to the hub from the crank. And Andrew has already shown this tends to be the case by directly applying torque to the cassette.
On the test wheel, the t-score for the offset is well in excess of 1 (the slope t-score is small, however). This is consistent with there being a fixed torque error in the hub. The two tests measured different offsets, but the separation between measured values is comparable to the standard error of either estimate, so there is no
statistical proof anything changed with an the offset. However, the probability of a wheel without an offset producing a similar set of results is very small.
So the conclusion? Saris didn't change anything. But beyond that I don't know. Next up: I need to get the wheel to someone with a spider-based power meter. A comparison with that, especially on a relatively steep climb, ridden with a smooth cadence at low speed, will be telling.
Anyone want a deal on a used Powertap?
Unfortunately I didn't follow up their quick return with a quick re-test. Honestly, I found it liberating to not have power numbers telling me how lame I was every single ride. It was fun to just ride. I didn't need the power meter to tell me if I was going hard or not.
But eventually I couldn't ignore it any longer. So time for the torque test, again.
My procedure was slightly modified, after what I'd seen a friend do with his. To optimize the crank orientation (the weight needs to hang perpendicular to the crank or the torque estimate will be off), I grabbed the rear wheel and rotated in, forward and backward, until I saw the Powertap torque reach a maximum value. But here I deviated from my friend's approach: instead of using this number, I grabbed the brakes, let things settle out, then used that number. So my data taken here, like data previously, were done with the brakes holding the wheel. My reasoning was I wanted to make sure the wheel was stationary, and the brakes could do this better than my hand holding the rear rim.
Okay, cut to the chase:
 Retested powertap, compared with previous test of my wheel and a reference ("C") wheel.
Retested powertap, compared with previous test of my wheel and a reference ("C") wheel.So it appears as if nothing has changed.
To test whether either wheel significantly deviates from the optimal curve, I did a t-test:
========== My wheel ===============The t-value is a test for significance: if it's less than 1, the
pre-service
Correlation coefficient = 0.110
Regression coefficient (SLOPE) = 0.008
Standard error of coefficient = 0.026
t - value for coefficient = 0.294
Regression constant (INTERCEPT) = -9.222
Standard error of constant = 2.829
t - value for constant = -3.260
post-service
Correlation coefficient = -0.061
Regression coefficient (SLOPE) = -0.004
Standard error of coefficient = 0.025
t - value for coefficient = -0.173
Regression constant (INTERCEPT) = -6.143
Standard error of constant = 2.769
t - value for constant = -2.219
====== Reference (C) wheel =========
Correlation coefficient = 0.300
Regression coefficient (SLOPE) = 0.011
Standard error of coefficient = 0.013
t - value for coefficient = 0.833
Regression constant (INTERCEPT) = -0.259
Standard error of constant = 1.596
t - value for constant = -0.162
result is generally consistent with random variation combined with the
actual value being zero.
So on the reference wheel, the t-value for both the offset and the deviation of slope from 1 have low t-values. This is what I'd expect, assuming all torque is transferred to the hub from the crank. And Andrew has already shown this tends to be the case by directly applying torque to the cassette.
On the test wheel, the t-score for the offset is well in excess of 1 (the slope t-score is small, however). This is consistent with there being a fixed torque error in the hub. The two tests measured different offsets, but the separation between measured values is comparable to the standard error of either estimate, so there is no
statistical proof anything changed with an the offset. However, the probability of a wheel without an offset producing a similar set of results is very small.
So the conclusion? Saris didn't change anything. But beyond that I don't know. Next up: I need to get the wheel to someone with a spider-based power meter. A comparison with that, especially on a relatively steep climb, ridden with a smooth cadence at low speed, will be telling.
Anyone want a deal on a used Powertap?

Comments
That's basically how I check my Quarq's torque slope. I use my old yellow cap PT Pro wheel as the "gauge" that tells me I'm at peak torque when raising the test weight off the floor. (BTW, that old PT Pro is ALWAYS within ~0.5% of the predicted torque for the weight...I guess I got a good one)
I used the raw number reported on the head unit (Cervo) in test mode before and after applying weight, averaged the two as my zero, and took the reading at optimized pedal orientation (orientation found moving rear wheel, reading taken holding rear brake) as the loaded number. The difference was the recorded torque, which the Cervo reports in in-lb.
8.85 lb-in = 1 N-m, so 32 units per N-m is better resolution for the Garmin than the Cervo.
Yeah, there's more absolute torque resolution with the CinQo/Garmin setup, but you also don't get to take advantage of the torque multiplication from the gearing like you do with a PT...
Oh...and I can't take credit for the idea of using the offsets to check the CinQo. That came to me from Jim Meyer himself ;-)