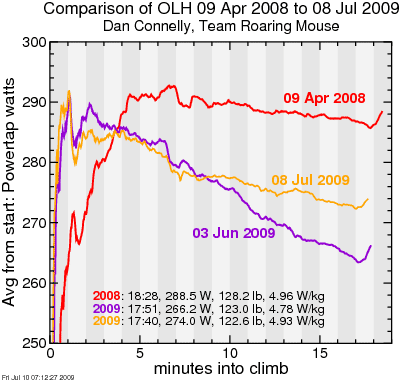
effect of road grade on VAM

VAM is an easy to calculate proxy for power-to-mass ratio commonly reported for professional riders in European races, where television coverage plus well documented hill profiles facilitates its extraction. VAM is the rate of altitude gained per unit time, for example in meters per hour. I recently recorded 1402 metters per hour in a break-through ride up Old La Honda, breaking my previous PR. The excellent Science of Sport Blog recently posted the following plot of some VAMs from recent Tour history: VAMs from the Tour de France, from The Science of Sport . Michele Ferrari's numerical calculation of the effect of road grade on VAM are often used as a reference, by me included, but an analytic form is perhaps more useful. I'll again assert a simplified, windless bike power-speed model, which is for "PowerTap power" neglecting drivetrain losses, but it is assumed drivetrain losses are a function of total power: p = f m m s + f w s³ , where p is a fixed power, ...